题目内容
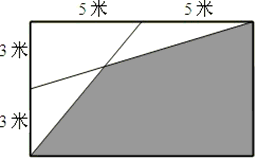
求图中阴影部分的面积是________平方米.
40
分析:如图所示,三角形1、2、3的面积和等于三角形1、3、4的面积和,且都等于15平方米,即等于长方形面积的 (长方形面积为60平方米);又因三角形3、4的面积相等,三角形1、2的面积相等,所以三角形1、2、3、4的面积都相等,且都等于所在大三角形的
(长方形面积为60平方米);又因三角形3、4的面积相等,三角形1、2的面积相等,所以三角形1、2、3、4的面积都相等,且都等于所在大三角形的 ,因此这4个三角形的面积是长方形面积的(
,因此这4个三角形的面积是长方形面积的(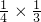 ),则4个三角形的面积和为长方形面积的(4×
),则4个三角形的面积和为长方形面积的(4×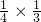 ),阴影部分的面积就等于长方形的面积减去4个小三角形的面积,问题得解.
),阴影部分的面积就等于长方形的面积减去4个小三角形的面积,问题得解.
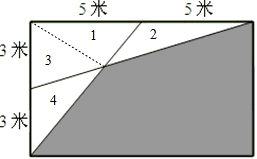
解答:由题意可知:S△1=S△2=S△3=S△4,
又因S△1+S△2+S△3=10×3÷2=15(平方米),
长方形的面积:10×6=60(平方米),
所以(S△1+S△2+S△3)是S长方形的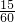 =
= ,
,
而S△1是(S△1+S△2+S△3)的 ,
,
则S△1是S长方形的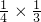 =
= ,
,
空白部分的面积就是长方形面积的4× =
= ,
,
则阴影部分的面积是长方形面积的1- =
= ,
,
所以阴影部分的面积=60× =40(平方米);
=40(平方米);
答:阴影部分的面积是40平方米.
故答案为:40.
点评:解答此题的关键是:求出每个小三角形的面积与长方形的面积关系,进而求得空白部分占长方形面积的几分之几,也就知道了阴影部分是长方形面积的几分之几,从而求解.
分析:如图所示,三角形1、2、3的面积和等于三角形1、3、4的面积和,且都等于15平方米,即等于长方形面积的
 (长方形面积为60平方米);又因三角形3、4的面积相等,三角形1、2的面积相等,所以三角形1、2、3、4的面积都相等,且都等于所在大三角形的
(长方形面积为60平方米);又因三角形3、4的面积相等,三角形1、2的面积相等,所以三角形1、2、3、4的面积都相等,且都等于所在大三角形的 ,因此这4个三角形的面积是长方形面积的(
,因此这4个三角形的面积是长方形面积的(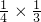 ),则4个三角形的面积和为长方形面积的(4×
),则4个三角形的面积和为长方形面积的(4×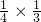 ),阴影部分的面积就等于长方形的面积减去4个小三角形的面积,问题得解.
),阴影部分的面积就等于长方形的面积减去4个小三角形的面积,问题得解.
解答:由题意可知:S△1=S△2=S△3=S△4,
又因S△1+S△2+S△3=10×3÷2=15(平方米),
长方形的面积:10×6=60(平方米),
所以(S△1+S△2+S△3)是S长方形的
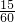 =
= ,
,而S△1是(S△1+S△2+S△3)的
 ,
,则S△1是S长方形的
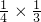 =
= ,
,空白部分的面积就是长方形面积的4×
 =
= ,
,则阴影部分的面积是长方形面积的1-
 =
= ,
,所以阴影部分的面积=60×
 =40(平方米);
=40(平方米);答:阴影部分的面积是40平方米.
故答案为:40.
点评:解答此题的关键是:求出每个小三角形的面积与长方形的面积关系,进而求得空白部分占长方形面积的几分之几,也就知道了阴影部分是长方形面积的几分之几,从而求解.

练习册系列答案
相关题目
 (2012?太原模拟)如图,六边形ABCDEF的面积是16平方厘米,M,N,P,Q分别是AB,CD,DE,AF的中点,求图中阴影部分的面积.
(2012?太原模拟)如图,六边形ABCDEF的面积是16平方厘米,M,N,P,Q分别是AB,CD,DE,AF的中点,求图中阴影部分的面积. (2011?苏州模拟)求图中阴影部分的面积.
(2011?苏州模拟)求图中阴影部分的面积.

