题目内容
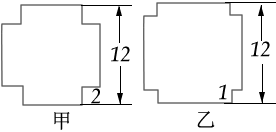
 在同样大小的正方形硬纸板的四个角上各剪去一个大小一样的小正方形,便可以做成一个没有盖的纸盒,按下面两种方法做出的纸盒中,哪一个容积大?大多少?请列式计算.(单位:dm)
在同样大小的正方形硬纸板的四个角上各剪去一个大小一样的小正方形,便可以做成一个没有盖的纸盒,按下面两种方法做出的纸盒中,哪一个容积大?大多少?请列式计算.(单位:dm)分析:计算铁盒的容积,需要求出盒子的边长,正方形硬纸板的边长都要减去两个2厘米即是盒子的底边边长,第一个盒子高是2厘米,第二个盒子高是1厘米.根据正方形的容积公式解答.
解答:解:根据题干分析可得:
第一个盒子的高为减去的小正方形的边长,即2厘米,
底边边长为大正方形的各边减去两个小正方形的边长,即12-2×2=8(分米),
所以第一个盒子的容积为82×2=128(立方分米);
第二个盒子的高为减去的小正方形的边长,即1厘米,
底边边长为大正方形的各边减去两个小正方形的边长,即12-1×2=10(分米),
所以第一个盒子的容积为102×1=100(立方分米),
128-100=28(立方分米),
答:第一个盒子容积大,大28立方分米.
第一个盒子的高为减去的小正方形的边长,即2厘米,
底边边长为大正方形的各边减去两个小正方形的边长,即12-2×2=8(分米),
所以第一个盒子的容积为82×2=128(立方分米);
第二个盒子的高为减去的小正方形的边长,即1厘米,
底边边长为大正方形的各边减去两个小正方形的边长,即12-1×2=10(分米),
所以第一个盒子的容积为102×1=100(立方分米),
128-100=28(立方分米),
答:第一个盒子容积大,大28立方分米.
点评:此题主要考查底面为正方形的长方体的体积公式的灵活运用.

练习册系列答案
相关题目

 下面5个图形都具有两个特点:
下面5个图形都具有两个特点: 在同样大小的正方形硬纸板的四个角上各剪去一个大小一样的小正方形,便可以做成一个没有盖的纸盒,按下面两种方法做出的纸盒中,哪一个容积大?大多少?请列式计算.(单位:dm)
在同样大小的正方形硬纸板的四个角上各剪去一个大小一样的小正方形,便可以做成一个没有盖的纸盒,按下面两种方法做出的纸盒中,哪一个容积大?大多少?请列式计算.(单位:dm)