题目内容
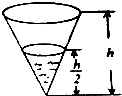 如图,圆椎形容器中装有3升水,水面高度正好是圆椎高度的一半,这个容器还能装________水.
如图,圆椎形容器中装有3升水,水面高度正好是圆椎高度的一半,这个容器还能装________水.
21升
分析:根据题意,可设容器中水的底面积为S1,圆锥形容器的底面积为S,可根据底面积的比等于高的平方的比计算出圆锥形容器的底面积与圆锥形内水的底面积的关系,然后再根据圆锥的体积公式计算出圆锥形容器的体积,再用圆锥形容器的体积减去水的体积就是还可以装的水的体积,列式解答即可得到答案.
解答:可设容器中水的底面积为S1,圆锥形容器的底面积为S,
 =
=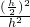 =
= ,即S=4S1,
,即S=4S1,
水的体积为:3= S1×
S1×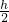 ,即S1h=18,
,即S1h=18,
容器的体积为: Sh=
Sh= ×4S1h
×4S1h
= ×4×18,
×4×18,
=6×4,
=24(升),
24-3=21(升),
答:这个容器还可以再装21升水.
故答案为:21升.
点评:解答此题的关键是确定容器的底面积与圆锥形水的底面积之间的关系,然后再根据圆锥的体积公式进行计算即可.
分析:根据题意,可设容器中水的底面积为S1,圆锥形容器的底面积为S,可根据底面积的比等于高的平方的比计算出圆锥形容器的底面积与圆锥形内水的底面积的关系,然后再根据圆锥的体积公式计算出圆锥形容器的体积,再用圆锥形容器的体积减去水的体积就是还可以装的水的体积,列式解答即可得到答案.
解答:可设容器中水的底面积为S1,圆锥形容器的底面积为S,
 =
=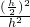 =
= ,即S=4S1,
,即S=4S1,水的体积为:3=
 S1×
S1×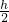 ,即S1h=18,
,即S1h=18,容器的体积为:
 Sh=
Sh= ×4S1h
×4S1h=
 ×4×18,
×4×18,=6×4,
=24(升),
24-3=21(升),
答:这个容器还可以再装21升水.
故答案为:21升.
点评:解答此题的关键是确定容器的底面积与圆锥形水的底面积之间的关系,然后再根据圆锥的体积公式进行计算即可.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2011?广州模拟)如图,圆椎形容器中装有3升水,水面高度正好是圆椎高度的一半,这个容器还能装
(2011?广州模拟)如图,圆椎形容器中装有3升水,水面高度正好是圆椎高度的一半,这个容器还能装