题目内容
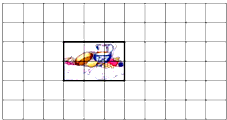 学校会议室的墙上贴着瓷砖,中间的6块组成了一个图案.在保持组合图案不变的情况下,有多少种不同的贴法?
学校会议室的墙上贴着瓷砖,中间的6块组成了一个图案.在保持组合图案不变的情况下,有多少种不同的贴法?
解:横着贴:前后每3行,竖着每2行就组成这个图形,所以贴法一共有:(11-2)×(6-1)=45(种),如果垂直翻转过来又是45种,共有45×2=90(种);
竖着贴:横着每3行,横着每2行就组成这个图形,贴法一共有:(6-2)×(11-1)=40(种),如果垂直翻转过来又是4种,共有40×2=80(种);
一共有:90+80=170(种).
答:有170种不同贴法.
分析:分四种情况:
横着贴:前后每3行,竖着每2行就组成这个图形,所以贴法一共有:(11-2)×(6-1)=45(种),如果垂直翻转过来又是45种,共有45×2=90(种);
竖着贴:横着每3行,横着每2行就组成这个图形,贴法一共有:(6-2)×(11-1)=40(种),如果垂直翻转过来又是4种,共有40×2=80(种);
最后将四种贴法加起来即可.
点评:解决本题的关键是分情况考虑,要做到不重不漏.
竖着贴:横着每3行,横着每2行就组成这个图形,贴法一共有:(6-2)×(11-1)=40(种),如果垂直翻转过来又是4种,共有40×2=80(种);
一共有:90+80=170(种).
答:有170种不同贴法.
分析:分四种情况:
横着贴:前后每3行,竖着每2行就组成这个图形,所以贴法一共有:(11-2)×(6-1)=45(种),如果垂直翻转过来又是45种,共有45×2=90(种);
竖着贴:横着每3行,横着每2行就组成这个图形,贴法一共有:(6-2)×(11-1)=40(种),如果垂直翻转过来又是4种,共有40×2=80(种);
最后将四种贴法加起来即可.
点评:解决本题的关键是分情况考虑,要做到不重不漏.

练习册系列答案
相关题目
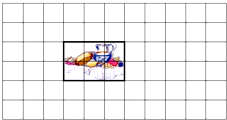 学校会议室的墙上贴着瓷砖,中间的6块组成了一个图案.在保持组合图案不变的情况下,有多少种不同的贴法?
学校会议室的墙上贴着瓷砖,中间的6块组成了一个图案.在保持组合图案不变的情况下,有多少种不同的贴法?