题目内容
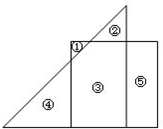 (2012?武汉模拟)一个等腰直角三角形和一个正方形如图摆放,①、②、③这三块的面积分别是2、8、58,则④、⑤这两块的面积差是
(2012?武汉模拟)一个等腰直角三角形和一个正方形如图摆放,①、②、③这三块的面积分别是2、8、58,则④、⑤这两块的面积差是8
8
.分析:由一个等腰直角三角形和一个正方形组成可知:①、②是等腰直角三角形,知面积可求得直角边,由此求得由①+③的宽,又可求①+③的面积(2+58),进一步求出①+③的长(也是正方形的边长).正方形的面积减去(①+③)求得⑤,再进一步求出等腰三角形的直角边(正方形的边长+②直角边),可得面积.用等腰直角三角形面积减去②③面积即可得④面积.⑤-④即可.
解答:解:①的面积是2,则其直角边长为2,②的面积是8,则其直角边长为4
①+③=2+58=60,因为③+①的宽为①直角边+②直角边=6,所以长为60÷6=10
由此可知正方形边长为10
⑤的面积为:10×10-(2+58)=40
等腰三角形边长为10+4=14
④的面积为:
×14×14-58-8=32
所以⑤-④为:40-32=8.
故答案为:8.
①+③=2+58=60,因为③+①的宽为①直角边+②直角边=6,所以长为60÷6=10
由此可知正方形边长为10
⑤的面积为:10×10-(2+58)=40
等腰三角形边长为10+4=14
④的面积为:
| 1 |
| 2 |
所以⑤-④为:40-32=8.
故答案为:8.
点评:此题主要抓住正方形和等腰三角形的性质,灵活利用面积与等边的关系解决问题.

练习册系列答案
相关题目