题目内容
求阴影部分的面积(单位:cm).
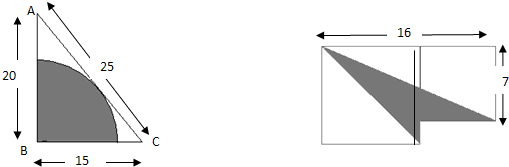
解:(1)15×20÷2×2÷25,
=300÷25,
=12(厘米);
 ×3.14×122,
×3.14×122,
= ×3.14×144,
×3.14×144,
=3.14×36,
=113.04(平方厘米);
答:阴影部分的面积是113.04平方厘米.
(2)(16-7)×(16-7)+7×7-(16-7)×(16-7)÷2-16×7÷2,
=9×9+49-9×9÷2-56,
=130-40.5-56,
=33.5(平方厘米);
答:阴影部分的面积是33.5平方厘米.
分析:(1)如图所示,作直角三角形ABC斜边AB上的高BD,且BD就为圆的半径,利用三角形的面积公式即可求出BD的长度,进而利用圆的面积公式即可求出阴影部分的面积.
(2)阴影部分的面积=大正方形的面积+小正方形的面积-空白部分的面积,代入数据即可求解.
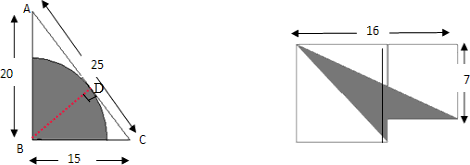
点评:解答此题的关键是弄清楚阴影部分的面积可以由哪些图形的面和或差求出.
=300÷25,
=12(厘米);
 ×3.14×122,
×3.14×122,=
 ×3.14×144,
×3.14×144,=3.14×36,
=113.04(平方厘米);
答:阴影部分的面积是113.04平方厘米.
(2)(16-7)×(16-7)+7×7-(16-7)×(16-7)÷2-16×7÷2,
=9×9+49-9×9÷2-56,
=130-40.5-56,
=33.5(平方厘米);
答:阴影部分的面积是33.5平方厘米.
分析:(1)如图所示,作直角三角形ABC斜边AB上的高BD,且BD就为圆的半径,利用三角形的面积公式即可求出BD的长度,进而利用圆的面积公式即可求出阴影部分的面积.
(2)阴影部分的面积=大正方形的面积+小正方形的面积-空白部分的面积,代入数据即可求解.

点评:解答此题的关键是弄清楚阴影部分的面积可以由哪些图形的面和或差求出.

练习册系列答案
相关题目
 图形计算:
图形计算:

 求阴影部分的面积(单位:厘米).
求阴影部分的面积(单位:厘米). 一个长方形被两条直线分成四个小长方形,其中三个的面积如图,求阴影部分的面积(单位:cm2).
一个长方形被两条直线分成四个小长方形,其中三个的面积如图,求阴影部分的面积(单位:cm2).