题目内容
我们把一个圆,平均分成若干份,拼成一个近似的长方形,它的长是
因为长方形的面积S=a×b,所以圆的面积S=
圆周长的一半
圆周长的一半
,宽是圆的半径
圆的半径
.因为长方形的面积S=a×b,所以圆的面积S=
2πr÷2
2πr÷2
×r
r
=πr2
πr2
.
分析:根据圆拼成的长方形的过程可知:近似长方形的长等于圆周长的一半,宽等于圆的半径,然后根据长方形的面积公式推导出圆的面积公式.据此解答.
解答:解:近似长方形的长是圆周长的一半,宽是圆的半径.
圆的面积=近似长方形的面积
=长×宽
=2πr÷2×r
=πr2.
故答案为:圆周长的一半,圆的半径,2πr÷2,r,πr2.
圆的面积=近似长方形的面积
=长×宽
=2πr÷2×r
=πr2.
故答案为:圆周长的一半,圆的半径,2πr÷2,r,πr2.
点评:本题主要考查了学生利用知识的迁移推导圆面积公式的过程.

练习册系列答案
相关题目
 如图:在推导圆面积公式的时候,我们把一个圆平均分成若干份,然后把它拼成一个近似的长方形.已知长方形的长是12.56厘米,原来圆的面积是多少平方厘米?
如图:在推导圆面积公式的时候,我们把一个圆平均分成若干份,然后把它拼成一个近似的长方形.已知长方形的长是12.56厘米,原来圆的面积是多少平方厘米? 把一个圆盘平均分成6份,随意转动转盘.
把一个圆盘平均分成6份,随意转动转盘.

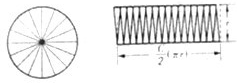 如图:在推导圆面积公式的时候,我们把一个圆平均分成若干份,然后把它拼成一个近似的长方形.已知长方形的长是12.56厘米,原来圆的面积是多少平方厘米?
如图:在推导圆面积公式的时候,我们把一个圆平均分成若干份,然后把它拼成一个近似的长方形.已知长方形的长是12.56厘米,原来圆的面积是多少平方厘米?