Question

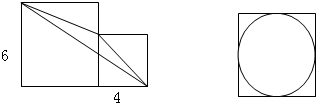
求左图三角形的面积是________（单位厘米）；右图正方形的面积为12平方厘米，圆的面积是________．

Answer 1

8    9.42平方厘米
分析：如图所示：（1）三角形ABD和三角形ABC等底等高，则二者的面积相等，都去掉公共部分（三角形ABE），则剩余部分的面积仍然相等，即三角形ADE和三角形EBC的面积相等，于是可得：三角形ADC与三角形DBC的面积相等，即等于小正方形的面积的一半，据此解答即可；
（2）设正方形的边长为a，则a²=12平方厘米，又因正方形的边长等于圆的直径，于是可以用正方形的边长表示出圆的面积，据此即可得解．
解答：（1）4×4÷2=8（平方厘米）；
答：左图三角形的面积是8平方厘米．
（2）设正方形的边长为a，
则a²=12平方厘米，
圆的面积为：3.14×，
=3.14×，
=3.14×3，
=9.42（平方厘米）；
答：圆的面积是9.42平方厘米．
故答案为：8、9.42平方厘米．
点评：解答此题的关键是弄清楚：所求图形的面积，可以由哪些图形的面积和或差求解，利用规则图形的面积和或差即可得解．