题目内容
在三角形ABC中,以三个顶点为圆心,1厘米为半径在三角形内画弧,得到三个扇形.
(1)如果∠A=115°,∠B=40°,∠C=25°,求这三个扇形的周长和.
(2)若不给三个角的角度,试求周长和.
(3)若果将三角形ABC换成任意凸N边形(既满足内角和=180×(n-2),求这N个扇形的周长和.
(1)如果∠A=115°,∠B=40°,∠C=25°,求这三个扇形的周长和.
(2)若不给三个角的角度,试求周长和.
(3)若果将三角形ABC换成任意凸N边形(既满足内角和=180×(n-2),求这N个扇形的周长和.
分析:(1)根据扇形的周长公式:C=弧长+2r,列式计算即可求解;
(2)根据三角形的内角和是180度,由乘法分配律可知这三个扇形的周长和是半径为1的半圆弧+半径×6,依此列式计算即可求解;
(3)根据N边形满足内角和是180×(n-2)求解,这N个扇形的周长和是半径为1的
圆弧+半径×2n,依此列式计算即可求解.
(2)根据三角形的内角和是180度,由乘法分配律可知这三个扇形的周长和是半径为1的半圆弧+半径×6,依此列式计算即可求解;
(3)根据N边形满足内角和是180×(n-2)求解,这N个扇形的周长和是半径为1的
| n-2 |
| 2 |
解答:解:(1)3.14×1×2×
+1×6,
=3.14+6,
=9.14(厘米).
答:这三个扇形的周长和是9.14厘米.
(2)3.14×1×2×
+1×6,
=3.14+6,
=9.14(厘米).
答:周长和是9.14厘米.
(3)3.14×1×2×
+1×2n,
=3.14n-6.28+2n,
=5.14n-6.28(厘米).
答:这N个扇形的周长和是(5.14n-6.28)厘米.
| 115+40+25 |
| 360 |
=3.14+6,
=9.14(厘米).
答:这三个扇形的周长和是9.14厘米.
(2)3.14×1×2×
| 180 |
| 360 |
=3.14+6,
=9.14(厘米).
答:周长和是9.14厘米.
(3)3.14×1×2×
| n-2 |
| 2 |
=3.14n-6.28+2n,
=5.14n-6.28(厘米).
答:这N个扇形的周长和是(5.14n-6.28)厘米.
点评:考查了巧算周长,本题关键是得到N个扇形的圆心角的和,从而求出N个扇形的弧长和.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (2012?明光市)①请在图1中画出三角形ABC中AB边上的高,并以AB边和AC边为平行四边形的两条邻边画一个平行四边形.
(2012?明光市)①请在图1中画出三角形ABC中AB边上的高,并以AB边和AC边为平行四边形的两条邻边画一个平行四边形.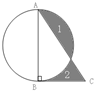 (2012?长清区模拟)在三角形abc中,∠c=90度,ab=20厘米,以ab为直径画圆.如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求bc的长度.
(2012?长清区模拟)在三角形abc中,∠c=90度,ab=20厘米,以ab为直径画圆.如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求bc的长度.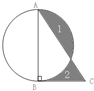 在三角形abc中,∠c=90度,ab=20厘米,以ab为直径画圆.如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求bc的长度.
在三角形abc中,∠c=90度,ab=20厘米,以ab为直径画圆.如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求bc的长度.