题目内容
某班学生不到50人,在一次测验中,有
的学生得优,
的学生得良,
的学生及格,那么,有
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 7 |
1
1
人不及格.分析:这班的人数应该是3、2、7的最小公倍数,而且的小于50;求出总人数,减去优、良和及格的人数,即可得解.
解答:解:2和3和7的最小公倍数是2×3×7=42,刚好小于50,
42÷(1-
-
-
)=42-14-21-6=1(人);
答:那么,有 1人不及格.
故答案为:1.
42÷(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 7 |
答:那么,有 1人不及格.
故答案为:1.
点评:此题考查了整除的性质,灵活应用整除,求出本班人数是解决此题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
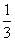 的学生得优,
的学生得优,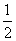 的学生得良,
的学生得良,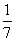 的学生得及格,则有( )人得优。
的学生得及格,则有( )人得优。