题目内容
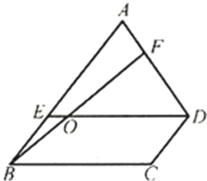 如图,在四边形ABCD中,AB=3BE,AD=3AF,四边形AEOF的面积是12,那么平行四边形BODC的面积是多少?
如图,在四边形ABCD中,AB=3BE,AD=3AF,四边形AEOF的面积是12,那么平行四边形BODC的面积是多少?分析:连接BD,因为AB=3BE,AD=3AF,根据高一定时,三角形的面积与底成正比例的性质可得:三角形BED的面积=
三角形ABD的面积;三角形ABF的面积=
三角形ABD的面积,由此即可得出三角形BED的面积=三角形ABF的面积,三角形BEO是它们的公共部分,所以可得三角形BOD的面积=四边形AEOF的面积=12,则再乘2,就是平行四边形BODC的面积.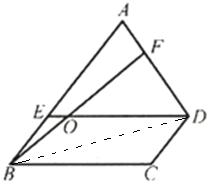
| 1 |
| 3 |
| 1 |
| 3 |

解答:解:连接BD,因为AB=3BE,所以三角形BED的面积=
三角形ABD的面积;
因为AD=3AF,三角形ABF的面积=
三角形ABD的面积;
所以三角形BED的面积=三角形ABF的面积,
所以三角形BOD的面积=四边形AEOF的面积=12,
则平行四边形BODC的面积是:12×2=24.
答:平行四边形的面积是24.
| 1 |
| 3 |
因为AD=3AF,三角形ABF的面积=
| 1 |
| 3 |
所以三角形BED的面积=三角形ABF的面积,
所以三角形BOD的面积=四边形AEOF的面积=12,
则平行四边形BODC的面积是:12×2=24.
答:平行四边形的面积是24.
点评:此题考查.高一定时,三角形的面积与底成正比的关系的灵活应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 (2010?常熟市模拟)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=
(2010?常熟市模拟)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE= 如图.在四边形ABCD中,AD=5cm,BC=9cm,∠ABC=∠BAD=90°,∠C=45°,四边形ABCD的面积是
如图.在四边形ABCD中,AD=5cm,BC=9cm,∠ABC=∠BAD=90°,∠C=45°,四边形ABCD的面积是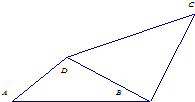 如图,在四边形ABCD中,∠ABC=∠ADB=105°,∠CDB=60°,∠CBD=75°,AB=CD=15厘米,四边形ABCD的面积是
如图,在四边形ABCD中,∠ABC=∠ADB=105°,∠CDB=60°,∠CBD=75°,AB=CD=15厘米,四边形ABCD的面积是