题目内容
直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE把梯形分成面积相等的两部分,DE长多少厘米?

分析:作EF⊥BC,DH⊥BC,又因为在直角梯形ABCD中,所以EF∥DH,四边形ABHD是一个长方形,AD=BH=3cm,DH=AB=4厘米,BC=6厘米,所以HC=3厘米,先求出EF、CD的长度,进一步求出DE的长度.
解答:解:画图如下:
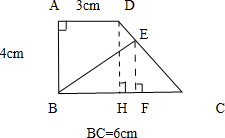
BE把梯形分成相等的两部分,△BCE面积=
梯形ABCD,
所以6×EF×
=(3+6)×4÷2÷2,
3EF=9,
3EF÷3=9÷3,
EF=3,
作EF⊥BC,DH⊥BC,
在直角梯形ABCD中,所以EF∥DH,四边形ABHD是一个长方形,
所以AD=BH=3cm,DH=AB=4cm,HC=BC-AD=3cm,
在直角△DHC中,CD=
42=
=5,
因为EF∥DH,
所以直角△CEF∽△DHC,
即,
=
,
所以CE=CD×EF÷DH,
CE=5×3÷4=
,
DE=CD-CE=5-
=
=1
(厘米),
答:DE 的长度是1
厘米.

BE把梯形分成相等的两部分,△BCE面积=
| 1 |
| 2 |
所以6×EF×
| 1 |
| 2 |
3EF=9,
3EF÷3=9÷3,
EF=3,
作EF⊥BC,DH⊥BC,
在直角梯形ABCD中,所以EF∥DH,四边形ABHD是一个长方形,
所以AD=BH=3cm,DH=AB=4cm,HC=BC-AD=3cm,
在直角△DHC中,CD=
| 2 | 32+ |
| 2 | 25 |
因为EF∥DH,
所以直角△CEF∽△DHC,
即,
| EF |
| DH |
| CE |
| CD |
所以CE=CD×EF÷DH,
CE=5×3÷4=
| 15 |
| 4 |
DE=CD-CE=5-
| 15 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
答:DE 的长度是1
| 1 |
| 4 |
点评:本题是一道超出小学范围的一道题目,考查了作垂线,平行线,三角形的相似,勾股定理等知识点.

练习册系列答案
相关题目

 如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中的阴影部分).若∠A=120°,AB=4cm,求梯形ABCD的高CD.
如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中的阴影部分).若∠A=120°,AB=4cm,求梯形ABCD的高CD.