题目内容
观察一列数：3，8，13，18，23，28，…．依此规律，在此数列中比2004大的最小整数是
2008
2008
．分析：观察给出的数列知道，此数列是一个首项是3，公差是5的等差数列，由此根据等差数列的通项公式an=a1+（n-1）×d，即可求出比2004大的最小整数．
解答：解：3+（n-1）×5＞2004，
5n-2＞2004，
5n＞2004+2，
5n＞2006，
n＞401.2；
所以n取402，
所以在此数列中比2004大的最小整数是：5×402-2=2010-2=2008；
故答案为：2008．
5n-2＞2004，
5n＞2004+2，
5n＞2006，
n＞401.2；
所以n取402，
所以在此数列中比2004大的最小整数是：5×402-2=2010-2=2008；
故答案为：2008．
点评：解答此题的关键是根据给出的数列知道是一个等差数列，由此根据等差数列的通项公式an=a1+（n-1）×q解决问题．
练习册系列答案
阅读快车系列答案
相关题目
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(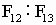
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。