题目内容
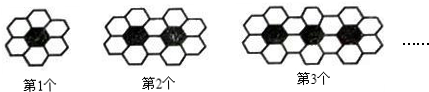
用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:
(1)第5个图案中有白色地面砖
(2)第n个图案中有白色地板砖
(1)第5个图案中有白色地面砖
22
22
块;(2)第n个图案中有白色地板砖
4n+2
4n+2
块.
分析:根据图形分析可得规律:每增加一个黑色六边形,则需增加4个白色六边形,即可得:第n个图案中共有6+4(n-1)个白色六边形.
解答:解:其中左边第一个黑色六边形与6个白色六边形相邻,
即每增加一个黑色六边形,则需增加4个白色六边形,则
第n个图案中共有白色六边形6+4×(n-1)=4n+2个,
故第n个图案中有白色地面砖(4n+2)块,
当n=5时:白色地面砖有:4×5+2=22(块).
故答案为:22;4n+2.
即每增加一个黑色六边形,则需增加4个白色六边形,则
第n个图案中共有白色六边形6+4×(n-1)=4n+2个,
故第n个图案中有白色地面砖(4n+2)块,
当n=5时:白色地面砖有:4×5+2=22(块).
故答案为:22;4n+2.
点评:此题考查了平面图形,主要培养学生的观察能力和空间想象能力,解题的关键是发现规律:多一个黑色六边形,多4个白色六边形.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
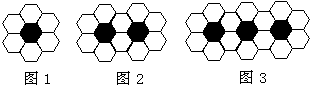 用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案: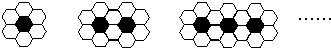
 用黑白两种颜色的正六边形地砖按如图的规律,拼成若干个图案,则第5个图案中白色地砖有
用黑白两种颜色的正六边形地砖按如图的规律,拼成若干个图案,则第5个图案中白色地砖有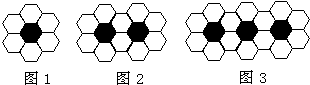 用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案: