题目内容
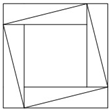
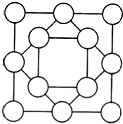 图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个项点上.
图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个项点上.(1)能否使8个三角形顶点上数字之和都相等?如果能,请给出填数方法:如果不能,请说明理由.
(2)能否使8个三角形顶点上数字之和各不相同?如果能,请给出填数方法;如果不能,请说明理由.
分析:(1)不能,如果能,则8个三角形顶点和的总数和应该是8的倍数,但是这个综合有三组1、2、3、4组成,其中一组数被计算三次,一组数被计算两次,一组数仅被计算一次,因此该总和的值为6,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等.
(2)能,见下图.
(2)能,见下图.
解答:解:(1)如果能,则8个三角形顶点和的总数和应该是8的倍数,但是这个综合有三组1、2、3、4组成,其中一组数被计算三次,一组数被计算两次,一组数仅被计算一次,因此该总和的值为6,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等.
(2)能,见下图.

(2)能,见下图.

点评:此题考查了数字和问题,有一定难度,应认真分析,进行推理,解决问题.

练习册系列答案
相关题目
 如图中有六个正方形,较小的正方形都由较大的正方形的四边中点连接而成.已知最大的正方形的边长为10厘米,那么最小的正方形的面积等于
如图中有六个正方形,较小的正方形都由较大的正方形的四边中点连接而成.已知最大的正方形的边长为10厘米,那么最小的正方形的面积等于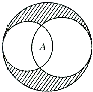 如图,图中有半径分别为5厘米,4厘米,3厘米,的三个圆,两小圆重叠部A的面积与阴影部分的面积相比,哪个大?
如图,图中有半径分别为5厘米,4厘米,3厘米,的三个圆,两小圆重叠部A的面积与阴影部分的面积相比,哪个大? 如图,有两个小正方体的六个面上分别写有1,2,3,4,5,6,如果随意抛掷这两个小正方体,那么它们落下后向上一面数字的和最大是多少?最小是多少?这些和中出现次数最多的数是多少?出现次数最多的这个数出现的可能性有多大?
如图,有两个小正方体的六个面上分别写有1,2,3,4,5,6,如果随意抛掷这两个小正方体,那么它们落下后向上一面数字的和最大是多少?最小是多少?这些和中出现次数最多的数是多少?出现次数最多的这个数出现的可能性有多大?