题目内容
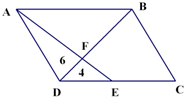 如图,E是平行四边形ABCD的CD边上的一点,BD与AE相交于点F,已知三角形AFD的面积是6,三角形DEF的面积是4,求四边形BCEF的面积.
如图,E是平行四边形ABCD的CD边上的一点,BD与AE相交于点F,已知三角形AFD的面积是6,三角形DEF的面积是4,求四边形BCEF的面积.分析:根据题干,要求四边形BCEF的面积,因为三角形DEF的面积是4,只要求得三角形DBC的面积即可解决问题.
(1)三角形AFD的面积是6,三角形DEF的面积是4,根据高一定时,三角形的面积与底成正比的性质可得:AF:EF=6:4=3:2;
(2)平行四边形ABCD中,AB:DE=AF:EF=3:2;AB=DC,所以DC:DE=3:2,由此利用高一定时,三角形的面积与底成正比的关系即可求出三角形DBC的面积,从而解决问题.
(1)三角形AFD的面积是6,三角形DEF的面积是4,根据高一定时,三角形的面积与底成正比的性质可得:AF:EF=6:4=3:2;
(2)平行四边形ABCD中,AB:DE=AF:EF=3:2;AB=DC,所以DC:DE=3:2,由此利用高一定时,三角形的面积与底成正比的关系即可求出三角形DBC的面积,从而解决问题.
解答:解:根据高一定时,三角形的面积与底成正比的性质可得:AF:EF=6:4=3:2;
又因为平行四边形ABCD中,三角形AFB与三角形DEF相似,所以AB:DE=AF:EF=3:2;
AB=DC,则DC:DE=3:2,
故三角形DBC的面积:三角形ADE的面积=3:2,
三角形ADE的面积为:6+4=10,
所以三角形DBC的面积为:3×10÷2=15,
所以四边形BCEF的面积是:15-4=11;
答:四边形BCEF的面积11.
又因为平行四边形ABCD中,三角形AFB与三角形DEF相似,所以AB:DE=AF:EF=3:2;
AB=DC,则DC:DE=3:2,
故三角形DBC的面积:三角形ADE的面积=3:2,
三角形ADE的面积为:6+4=10,
所以三角形DBC的面积为:3×10÷2=15,
所以四边形BCEF的面积是:15-4=11;
答:四边形BCEF的面积11.
点评:根据题干把要求的四边形BCEF的面积转化成计算三角形DBC的面积是解决本题的关键.此题考查了利用高一定时三角形的面积与底成正比的性质和平行线间对应线段成比例的性质解决计算三角形面积的灵活应用.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
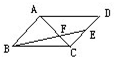 如图,E是平行四边形ABCD边CD的中点,AC和BE相交于F,如果三角形EFC的面积是1平方厘米,则平行四边形ABCD的面积是
如图,E是平行四边形ABCD边CD的中点,AC和BE相交于F,如果三角形EFC的面积是1平方厘米,则平行四边形ABCD的面积是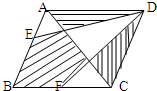 如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为
如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为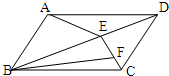 如图:ABCD是平行四边形,E是对角线BD上的一点,EF=2FC.如果三角形ABE的面积是8平方厘米,那么三角形BCF的面积是
如图:ABCD是平行四边形,E是对角线BD上的一点,EF=2FC.如果三角形ABE的面积是8平方厘米,那么三角形BCF的面积是