题目内容
一个长方体木块,它的所有棱长之和为36分米,它的长、宽、高之比为2:3:4,现在要将这个长方体削减一个体积最大的圆柱体,这个圆柱体的体积是________立方分米.
14.13
分析:根据棱长之和先求出一条长、宽、高的和是36÷4=9厘米,根据比的性质分别求出这个长方体的长、宽、高,再利用长方体内切割最大圆柱的方法即可解答.
解答:36÷4=9(厘米),
4+3+2=9,
所以长方体的长是:9× =2(分米),
=2(分米),
长方体的宽是:9×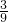 =3(分米),
=3(分米),
长方体的高是:9× =4(分米),
=4(分米),
将这个长方体削成一个体积最大的圆柱体,有以下三种削法:
(1)以3分米为底面直径,以2分米为圆柱的高,体积为:
3.14×( )2×2,
)2×2,
=3.14× ×2,
×2,
=14.13(立方分米),
(2)以2分米为底面直径,以4分米为高,体积为:
3.14×( )2×4,
)2×4,
=3.14×1×4,
=12.56(立方分米),
(3)以2分米为底面直径,以3分米为高,体积为:
3.14×( )2×3,
)2×3,
=3.14×1×3,
=9.42(立方分米).
答:这个圆柱体的体积是14.13立方分米.
故答案为:14.13.
点评:此题要抓住长方体内最大的圆柱的切割特点,分情况计算比较.
分析:根据棱长之和先求出一条长、宽、高的和是36÷4=9厘米,根据比的性质分别求出这个长方体的长、宽、高,再利用长方体内切割最大圆柱的方法即可解答.
解答:36÷4=9(厘米),
4+3+2=9,
所以长方体的长是:9×
 =2(分米),
=2(分米),长方体的宽是:9×
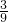 =3(分米),
=3(分米),长方体的高是:9×
 =4(分米),
=4(分米),将这个长方体削成一个体积最大的圆柱体,有以下三种削法:
(1)以3分米为底面直径,以2分米为圆柱的高,体积为:
3.14×(
 )2×2,
)2×2,=3.14×
 ×2,
×2,=14.13(立方分米),
(2)以2分米为底面直径,以4分米为高,体积为:
3.14×(
 )2×4,
)2×4,=3.14×1×4,
=12.56(立方分米),
(3)以2分米为底面直径,以3分米为高,体积为:
3.14×(
 )2×3,
)2×3,=3.14×1×3,
=9.42(立方分米).
答:这个圆柱体的体积是14.13立方分米.
故答案为:14.13.
点评:此题要抓住长方体内最大的圆柱的切割特点,分情况计算比较.

练习册系列答案
相关题目