题目内容
把边长为1厘米的正方形纸片按下面的规律拼搭:
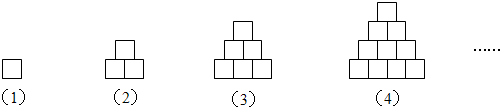
①那么第5个图形应该由几张正方形纸片拼成?
②第10个图形的周长是多少厘米?
③如果拼成的图形的周长是 200厘米,那么它是由几张正方形纸片拼成的?
解:(1)根据题干分析可得:第n个图形有n层,则小正方形个数是按1+2+3+…+n排列的;
所以第五个图形的正方形个数为:1+2+3+4+5=15(个);
答:第5个图形应该由15张正方形纸片拼成.
(2)根据题干分析可得:第n个图形周长就是:n×4=4n(厘米),
所以第10个图形的周长是:10×4=40(厘米),
答:第10个图形的周长是40厘米.
(3)根据(1)(2)中推理的结论可得:
200÷4=50(个),即这是第50个图形;
1+2+3+…+50=(50+1)×(50÷2)=51×25=1275(个),
答:周长是 200厘米的图形是由1275张正方形纸片拼成的.
分析:(1)根据图形中小正方形的个数来看,第一个图形只有1层,是1个正方形;第二个图形有2层,小正方形个数从上面开始按1+2的顺序排列;第三个图形有3层,小正方形个数是按1+2+3排列的;第四个图形有4层,小正方形个数是按1+2+3+4的顺序排列的…所以第n个图形有n层,小正方形个数是按1+2+3+…+n排列的;所以第五个图形是由1+2+3+4+5=(15)个正方形组成.
(2)根据题干观察可得:第一个图形周长是1×4=4(厘米),第二个图形周长是2×4=8(厘米),第三个图形周长是3×4=12(厘米),第四个图形周长是4×4=16(厘米)…则第n个图形周长就是n×4=4n(厘米),由此即可求得第10个图形的周长.
(3)利用上题(2)中推理得出的结论:即可求出周长为200的图形是第(200÷4=50)个图形,利用(1)中推理的结论可得:第50个图形中,小正方形的个数为:1+2+3+…+50,利用高斯求和的方法即可简便计算得出答案.
点评:解决此类问题,都要抓住题干中的图形排列特点和数量变化特点,从特殊例子推理得出一般结论,然后利用推理得出的结论解决问题.这里主要培养学生的观察和推理、归纳的能力.
所以第五个图形的正方形个数为:1+2+3+4+5=15(个);
答:第5个图形应该由15张正方形纸片拼成.
(2)根据题干分析可得:第n个图形周长就是:n×4=4n(厘米),
所以第10个图形的周长是:10×4=40(厘米),
答:第10个图形的周长是40厘米.
(3)根据(1)(2)中推理的结论可得:
200÷4=50(个),即这是第50个图形;
1+2+3+…+50=(50+1)×(50÷2)=51×25=1275(个),
答:周长是 200厘米的图形是由1275张正方形纸片拼成的.
分析:(1)根据图形中小正方形的个数来看,第一个图形只有1层,是1个正方形;第二个图形有2层,小正方形个数从上面开始按1+2的顺序排列;第三个图形有3层,小正方形个数是按1+2+3排列的;第四个图形有4层,小正方形个数是按1+2+3+4的顺序排列的…所以第n个图形有n层,小正方形个数是按1+2+3+…+n排列的;所以第五个图形是由1+2+3+4+5=(15)个正方形组成.
(2)根据题干观察可得:第一个图形周长是1×4=4(厘米),第二个图形周长是2×4=8(厘米),第三个图形周长是3×4=12(厘米),第四个图形周长是4×4=16(厘米)…则第n个图形周长就是n×4=4n(厘米),由此即可求得第10个图形的周长.
(3)利用上题(2)中推理得出的结论:即可求出周长为200的图形是第(200÷4=50)个图形,利用(1)中推理的结论可得:第50个图形中,小正方形的个数为:1+2+3+…+50,利用高斯求和的方法即可简便计算得出答案.
点评:解决此类问题,都要抓住题干中的图形排列特点和数量变化特点,从特殊例子推理得出一般结论,然后利用推理得出的结论解决问题.这里主要培养学生的观察和推理、归纳的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目