题目内容
用黑白两种颜色的正六边形地板砖按如图所示的规律拼成若干个图案,那么第10个图案中有白色地板砖
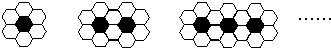
42
42
块,第n个图案中有白色地板砖(4n+2)
(4n+2)
块.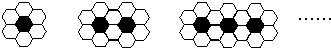
分析:由已知图形可以发现:前三个图形中白色地砖的块数分别为:6,10,14,所以可以发现每一个图形都比它前一个图形多4个白色地砖,所以可以得到第n个图案有白色地面砖4n+2块.
解答:解:第1个图有白色块4+2,第2图有4×2+2,第3个图有4×3+2,
所以第10个图应该有4×10+2=42块,
第n个图应该有(4n+2)块.
故答案为:42,(4n+2).
所以第10个图应该有4×10+2=42块,
第n个图应该有(4n+2)块.
故答案为:42,(4n+2).
点评:此题考查了数与形结合的规律,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
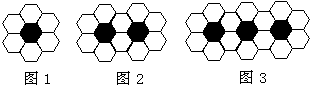 用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案: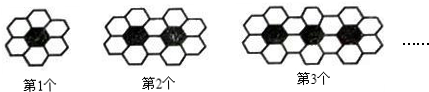
 用黑白两种颜色的正六边形地砖按如图的规律,拼成若干个图案,则第5个图案中白色地砖有
用黑白两种颜色的正六边形地砖按如图的规律,拼成若干个图案,则第5个图案中白色地砖有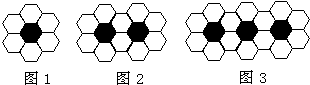 用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案: