题目内容
 如图,在△ABC中,AB=AC,AD=BD=BC,那么∠A=
如图,在△ABC中,AB=AC,AD=BD=BC,那么∠A=36
36
度.分析:由AB=AC,AD=BD=BC,根据等角对等边的知识,可得∠A=∠ABD,∠C=∠ABC=∠CDB,设∠A=x°,根据等腰三角形的性质得出∠ABD=x°,∠C=∠ABC=∠CDB=2x°,然后根据三角形的内角和定理得出关于x的方程,解方程即可求得答案.
解答:解:因为AB=AC,AD=BD=BC,
所以∠A=∠ABD,∠C=∠ABC=∠CDB,
设∠A=x°,则∠ABD=∠A=x°,
因为∠C=∠ABC=∠CDB=∠A+∠ABD=2x°
所以∠A+∠C+∠ABC=180°,
所以x+2x+2x=180,
解得x=36.
故等腰三角形ABC的顶角度数为36°.
故答案为:36.
所以∠A=∠ABD,∠C=∠ABC=∠CDB,
设∠A=x°,则∠ABD=∠A=x°,
因为∠C=∠ABC=∠CDB=∠A+∠ABD=2x°
所以∠A+∠C+∠ABC=180°,
所以x+2x+2x=180,
解得x=36.
故等腰三角形ABC的顶角度数为36°.
故答案为:36.
点评:本题考查了三角形的内角和定理,三角形的外角性质,等腰三角形的性质等知识,此题难度适中,解题的关键是掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,在△ABC中,D为BC边上任一点,AE=
如图,在△ABC中,D为BC边上任一点,AE= 如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE=
如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE= (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?
如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?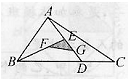 如图,在△ABC中,
如图,在△ABC中,