Question

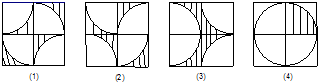下面有四个图形，正方形大小相等，阴影部分面积也相等的图有

1. A.
   （1）、（2）、（3）
2. B.
   （2）、（3）、（4）
3. C.
   （1）、（3）、（4）
4. D.
   （1）、（2）、（4）

Answer 1

A
分析：根据题意，图（1）、（2）、（3）中空白部分的图形可以分别组成一个以正方形的边长为直径的圆，阴影部分的面积可用正方形的面积减去里面最大圆的面积即可，图（4）中的阴影部分的面积就是正方形内最大圆的面积的，可设正方形的边长为2，根据正方形的面积公式和圆的面积公式进行计算即可得到各个图形中阴影部分的面积，然后再进行比较即可得到答案．
解答：设正方形的边长为2，
正方形的面积为：2×2=4，
正方形内最大圆的半径就为：2÷2=1，
里面最大圆的面积为：πr²=π1²=π，
图（1）、（2）、（3）阴影部分的面积为：
4-π1²=4-π，
图（4）中阴影部分的面积为：×1²π=，
答：阴影部分面积相等的图形有（1）、（2）、（3）．
故答案为：A．
点评：此题主要考查的是正方形的面积公式和圆的面积公式的应用．