题目内容
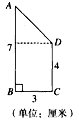
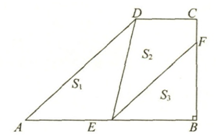 下图中ABCD是一个直角梯形,其上底CD=3厘米,下底AB=9厘米,线段DE、EF把梯形分成面积相等的3块,S1、S2和S3,已知CF=2厘米,那么直角梯形ABCD的面积是多少?
下图中ABCD是一个直角梯形,其上底CD=3厘米,下底AB=9厘米,线段DE、EF把梯形分成面积相等的3块,S1、S2和S3,已知CF=2厘米,那么直角梯形ABCD的面积是多少?分析:要求梯形ABCD的面积,必需求出高BC的长度,假设BC的长度为x厘米,因为S1=S2=S3=6x÷3=2x(平方厘米),又因为AE=S1×2÷BC=2x×2÷x=4厘米,EB=AB-AE=9-4=5厘米,又因为三角形AED和三角形EBF的面积相等,列方程即可求出BC的长度,进而即可求出梯形的面积.
解答:解:设BC=x厘米,
梯形ABCD的面积=(3+9)x=6x(平方厘米),
S1=S2=S3=6x÷3=2x(平方厘米),
AE=2x×2÷x=4(厘米),EB=9-4=5(厘米);
2x=5(x-2)×
,
2x=
(x-2),
2x=
x-5,
(
-2)x=5,
x=5,
x=5×2,
x=10;
则梯形的面积为:6×10=60(平方厘米).
答:梯形的面积为60平方厘米.
梯形ABCD的面积=(3+9)x=6x(平方厘米),
S1=S2=S3=6x÷3=2x(平方厘米),
AE=2x×2÷x=4(厘米),EB=9-4=5(厘米);
2x=5(x-2)×
| 1 |
| 2 |
2x=
| 5 |
| 2 |
2x=
| 5 |
| 2 |
(
| 5 |
| 2 |
| 1 |
| 2 |
x=5×2,
x=10;
则梯形的面积为:6×10=60(平方厘米).
答:梯形的面积为60平方厘米.
点评:解决本题的关键是根据三角形AED和三角形EBF的面积相等解出BC的长度.

练习册系列答案
相关题目
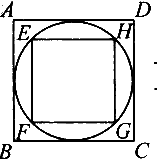
 如下图,已知正方形ABCD的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连接起来得到上图.那么图中阴影部分的总面积是
如下图,已知正方形ABCD的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连接起来得到上图.那么图中阴影部分的总面积是
 →
→ 
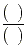 。
。