题目内容
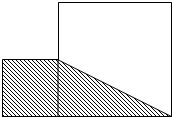如图，两个大小不等的正方形拼成一个图形，已知小正方形的边长是4厘米，阴影部分的面积是30平方厘米，求空白部分的面积是多少？．
解：设大正方形的边长为a，
由题意可得：（4+4+a）×4÷2=30，
（8+a）×4÷2=30，
（8+a）×4=60，
8+a=15，
a=7，
空白部分的面积：（7-4+7）×7÷2，
=10×7÷2，
=35（平方厘米）；
答：空白部分的面积是35平方厘米．
分析：设大正方形的边长为a，由题意可得：（4+4+a）×4÷2=30，据此即可求出大正方形的边长，进而再据梯形的面积公式即可求解．
点评：利用梯形的面积公式求出大正方形边长，是解答本题的关键．
由题意可得：（4+4+a）×4÷2=30，
（8+a）×4÷2=30，
（8+a）×4=60，
8+a=15，
a=7，
空白部分的面积：（7-4+7）×7÷2，
=10×7÷2，
=35（平方厘米）；
答：空白部分的面积是35平方厘米．
分析：设大正方形的边长为a，由题意可得：（4+4+a）×4÷2=30，据此即可求出大正方形的边长，进而再据梯形的面积公式即可求解．
点评：利用梯形的面积公式求出大正方形边长，是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
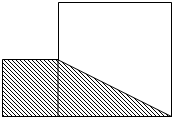如图，两个大小不等的正方形拼成一个图形，已知小正方形的边长是4厘米，阴影部分的面积是30平方厘米，求空白部分的面积是多少？．
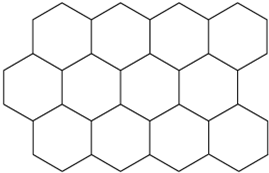卡纸上编号1～4的图形均是由数量不等的相同大小的正六边形组成的．请完成以下问题：