题目内容
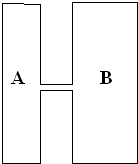 (2013?广州模拟)A和B都是高度为10厘米的圆柱形容器(如图所示),底面半径分别为1厘米和2厘米.一水龙头单独向A注水,用1分钟可以注满.现在两个容器在它们高度一半处用一个细管连通(连通管子的容积忽略不计),仍用该龙头向A注水.问:
(2013?广州模拟)A和B都是高度为10厘米的圆柱形容器(如图所示),底面半径分别为1厘米和2厘米.一水龙头单独向A注水,用1分钟可以注满.现在两个容器在它们高度一半处用一个细管连通(连通管子的容积忽略不计),仍用该龙头向A注水.问:(1)2分钟时,容器A中的高度是多少?
(2)3分钟时,容器A中水的高度是多少?
分析:根据圆柱的体积公式v=sh,求出A容器的容积,3.14×12×10=31.4立方厘米,已知B容器的底面半径是A容器的2倍,高相等,B容器的容积就是A容器的4倍;那么要把两个容器都注满一共需要1+4=5分钟,已知现在两个容器在它们高度一半处用一个细管连通,2分钟后A中的水高(10÷2)=5厘米(其余的水流到B容器了);由此可知,用2.5分钟的时间两个容器中的水的高度相等,都是5厘米;以后的时间两个容器中的水位同时上升,用3分钟注入水的体积除以两个容器的底面积之和问题得到解决.
解答:解:(1)A容器的容积是:
3.14×12×10=31.4(立方厘米);
已知B容器的底面半径是A容器的2倍,高相等,B容器的容积就是A容器的4倍;
那么要把两个容器都注满一共需要1+4=5(分钟),已知现在两个容器在它们高度一半处用一个细管连通,2分钟后A中的水高(10÷2)=5厘米(其余的水流到B容器了);由此可知,用2.5分钟的时间两个容器中的水的高度相等,都是5厘米;
(2)两个容器的底面积之和是:
3.14×12+3.14×22
=3.14+12.56
=15.7(平方厘米);
3分钟注入的水是:
31.4×3=94.2(立方厘米);
94.2÷15.7=6(厘米);
答:2分钟时,容器A中的高度是5厘米,3分钟时,容器A中水的高度是6厘米.
3.14×12×10=31.4(立方厘米);
已知B容器的底面半径是A容器的2倍,高相等,B容器的容积就是A容器的4倍;
那么要把两个容器都注满一共需要1+4=5(分钟),已知现在两个容器在它们高度一半处用一个细管连通,2分钟后A中的水高(10÷2)=5厘米(其余的水流到B容器了);由此可知,用2.5分钟的时间两个容器中的水的高度相等,都是5厘米;
(2)两个容器的底面积之和是:
3.14×12+3.14×22
=3.14+12.56
=15.7(平方厘米);
3分钟注入的水是:
31.4×3=94.2(立方厘米);
94.2÷15.7=6(厘米);
答:2分钟时,容器A中的高度是5厘米,3分钟时,容器A中水的高度是6厘米.
点评:此题主要考查圆柱的体积(容积)的计算,解答关键是理解现在两个容器在它们高度一半处用一个细管连通,当A中的水高是容器高的一半时,其余的水流到B容器了;以后的时间两个容器中的水位同时上升,用3分钟注入水的体积除以两个容器的底面积之和问题得到解决.

练习册系列答案
相关题目