Question

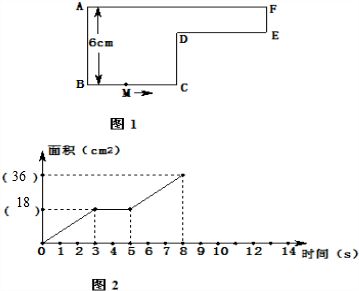
一只蚂蚁从图1中的点B开始，按逆时针方向沿着图形边框爬到点A，速度是2cm/s．∠A=∠B=∠C=∠D=∠E=∠F=90°．如果将蚂蚁当作点M，那么它与AB连成了一个三角形ABM，△ABM的面积随着蚂蚁爬动时间的变化而变化（如图2）．若8秒时，△ABM的面积最大，请将图2补充完整．

Answer 1

分析：根据题意，在0--3时间段，三角形面积逐渐增大，所以BC=2×3=6cm，则在3秒时△ABM的面积=6×6÷2=18（平方厘米）；
在3--5时间段，三角形面积不变，所以CD=2×2=4（cm）；
在5--8时间段，三角形面积逐渐增大，所以DE=2×3=6（cm），则在8秒时△ABM的面积=6×（6+6）÷2=36（平方厘米）；
现在，下面图中两个括号可以填了．
因为CD=4，AB=6，所以EF=AB-CD=2，2÷2=1则在8秒后又经过1秒，三角形面积不变，8--9时间段画一条横线；
AF=BC+DE=12，12÷2=6，蚂蚁又经过6秒到达A点，且在A点时面积为0，则在9--15时间段，画一条斜线，且在15秒时面积为0．

解答：解：BC=2×3=6cm，
所以则在3秒时△ABM的面积=6×6÷2=18（平方厘米）；
CD=2×2=4（cm）；
DE=2×3=6（cm），
所以在8秒时△ABM的面积=6×（6+6）÷2=36（平方厘米）；
答：当小蚂蚁爬到3秒时，三角形△ABM的面积是18平方厘米，当小蚂蚁爬到8秒时，三角形△ABM的面积是36平方厘米．
作图如下：

故答案为：18，36．

点评：解答此题的关键是确定图形各条线段的长度，然后再根据折线统计图的趋势进行解答即可．