题目内容
如图,一张桌子可以坐4人,两张桌子并起来可以坐6人,三张桌子并起来可以坐8人.像这样多少张桌子并起来可以坐40人?
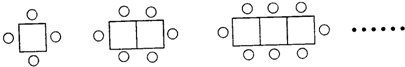
- A.17张
- B.18张
- C.19张
- D.20张
C
分析:一张桌子坐4人,两张桌子做6人,三张坐8人…
第一张坐4人,以后每增加1张桌子就增加2人;
所以n张桌子坐4+(n-1)×2人;求出当能做40人时n的值即可.
解答:设像这样n张桌子并起来可以坐40人,由题意可知:
4+(n-1)×2=40,
4+2n-2=40,
2n+2=40,
2n=38,
n=19;
答:像这样19张桌子并起来可以坐40人.
故选:C.
点评:解决本题关键是根据给出的桌子数和人数,找出人数随桌子数变化的规律,写出通项公式,进而求解.
分析:一张桌子坐4人,两张桌子做6人,三张坐8人…
第一张坐4人,以后每增加1张桌子就增加2人;
所以n张桌子坐4+(n-1)×2人;求出当能做40人时n的值即可.
解答:设像这样n张桌子并起来可以坐40人,由题意可知:
4+(n-1)×2=40,
4+2n-2=40,
2n+2=40,
2n=38,
n=19;
答:像这样19张桌子并起来可以坐40人.
故选:C.
点评:解决本题关键是根据给出的桌子数和人数,找出人数随桌子数变化的规律,写出通项公式,进而求解.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 (2008?天宁区)一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人(如图).像这样( )张桌子拼起来可以坐24人.
(2008?天宁区)一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人(如图).像这样( )张桌子拼起来可以坐24人.
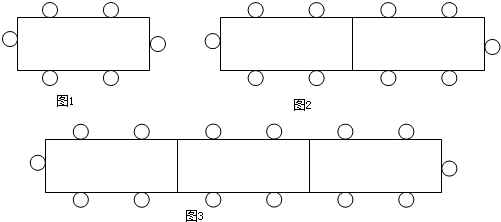
 一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人(如图).像这样____张桌子拼起来可以坐24人.
一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人(如图).像这样____张桌子拼起来可以坐24人.