题目内容
 如图,在一张2009×2009的方格纸上,将每个方格所在的行数和列数加起来,填在这个方格中,如a=3+3=6,b=2006+4=2010,c=2+2007=2009,则填入的这2009×2009=4036081个数中,偶数比奇数
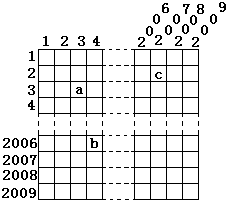
如图,在一张2009×2009的方格纸上,将每个方格所在的行数和列数加起来,填在这个方格中,如a=3+3=6,b=2006+4=2010,c=2+2007=2009,则填入的这2009×2009=4036081个数中,偶数比奇数多
多
(填“多”或“少”),偶数与奇数个数的差是1
1
.分析:通过观察可知,每两个相邻的方格,所填的数一奇一偶,将第一行的每个方格与它下面的相邻方格配对,如第一行,第一列为1+1=2,第二行第一列为1+2=3,…,由此可知,第一、二行中奇数与偶数正好一样多.同理,前2008行中奇数与偶数一样多.第2009行的前2008个方格也可两两配对,每对相邻的方格中的数一奇一偶,所以这2008格中的奇数偶数也一样多.最后,第2009行,第2009列即最后一个方格填2009+2009=4018,为偶数,所以4036081个数中,偶数恰好比奇数多1个.
解答:解:通过观察,可以发现如下规律:
每两个相邻的方格,所填的数为一奇一偶,
由此可知,偶数行中的奇数与偶数的个数应一样多,
如第一、二行中奇数与偶数正好一样多.同理,前2008行中奇数与偶数一样多.
共有2009行,
第2009行的前2008个方格中的数字奇偶性也可两两配对,
所以这2008格中的奇数偶数也一样多.
最后,第2009行,第2009列即最后一个方格填2009+2009=4018,为偶数.
所以4036081个数中,偶数比奇数多,恰好比奇数多1个.
故答案为:多,1.
每两个相邻的方格,所填的数为一奇一偶,
由此可知,偶数行中的奇数与偶数的个数应一样多,
如第一、二行中奇数与偶数正好一样多.同理,前2008行中奇数与偶数一样多.
共有2009行,
第2009行的前2008个方格中的数字奇偶性也可两两配对,
所以这2008格中的奇数偶数也一样多.
最后,第2009行,第2009列即最后一个方格填2009+2009=4018,为偶数.
所以4036081个数中,偶数比奇数多,恰好比奇数多1个.
故答案为:多,1.
点评:通过观察发现,每两个相邻的方格,所填的数为一奇一偶的排列规律并由此得出偶数行中的奇数与偶数的个数应一样多的结论是完成本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
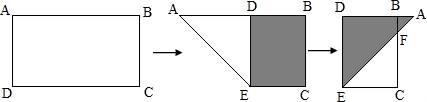
 (2009?雁江区)用一张长45cm,宽35cm的长方形彩纸.请你计划剪成每张长15cm,宽10cm的长方形贺年卡.
(2009?雁江区)用一张长45cm,宽35cm的长方形彩纸.请你计划剪成每张长15cm,宽10cm的长方形贺年卡.