题目内容
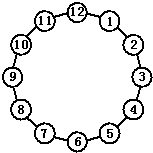 如图,一个圆盘上均匀地依次表示第1、2、3、…、12个洞.有一只小虫从1号洞按顺时针方向起跳,规定它跳的步数是它起跳洞的数码.例如,第1次从第1洞跳到第1洞,第2次从第2洞跳2步到第4洞,第3次从第4洞起跳,跳4步到第8洞,….第m次从第x洞起跳,跳x步,如果小虫按照这个规则从第1洞起跳,跳了100次到第N(N=1、2、3、…12)洞,则它共跳了多少步?N是几?
如图,一个圆盘上均匀地依次表示第1、2、3、…、12个洞.有一只小虫从1号洞按顺时针方向起跳,规定它跳的步数是它起跳洞的数码.例如,第1次从第1洞跳到第1洞,第2次从第2洞跳2步到第4洞,第3次从第4洞起跳,跳4步到第8洞,….第m次从第x洞起跳,跳x步,如果小虫按照这个规则从第1洞起跳,跳了100次到第N(N=1、2、3、…12)洞,则它共跳了多少步?N是几?分析:起跳的洞号分别是:1,2,4,8,4,8,4,8,4,8,…
到达的洞号分别是:2,4,8,4,8,4,8,…
跳的步数分别是1,2,4,8,4,8,…
根据上面的循环,运用列表法进行求解.
到达的洞号分别是:2,4,8,4,8,4,8,…
跳的步数分别是1,2,4,8,4,8,…
根据上面的循环,运用列表法进行求解.
解答:解:根据题意,得小表:
由上表可知,除了第1、2次,从第3次开始,跳的步数以4步、8步周期循环.且第100次到达洞序号为“4”号洞,即N是“4”.
小虫共跳了:1+2+(100-2)÷2×(4+8)=591(步)
答:它共跳了591步,N是4.
| 次数 | 起跳洞序号 | 到达洞序号 | 跳的步数 |
| 1 | 1 | 2 | 1 |
| 2 | 2 | 4 | 2 |
| 3 | 4 | 8 | 4 |
| 4 | 8 | 4 | 8 |
| 5 | 4 | 8 | 4 |
| 6 | 8 | 4 | 8 |
| … | … | … | … |
| 99 | 4 | 8 | 4 |
| 100 | 8 | 4 | 8 |
小虫共跳了:1+2+(100-2)÷2×(4+8)=591(步)
答:它共跳了591步,N是4.
点评:先根据洞号和跳的方法,找出循环的规律,再根据规律求解.

练习册系列答案
相关题目
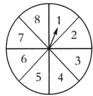 如图为一个被均匀分成8个部分的圆盘,旋转圆盘,圆盘停止后,指针落在奇数上的可能性是
如图为一个被均匀分成8个部分的圆盘,旋转圆盘,圆盘停止后,指针落在奇数上的可能性是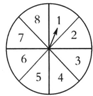 如图为一个被均匀分成8个部分的圆盘,旋转圆盘,圆盘停止后,指针落在奇数上的可能性是________.
如图为一个被均匀分成8个部分的圆盘,旋转圆盘,圆盘停止后,指针落在奇数上的可能性是________.