题目内容
 如图,三角形ABC的面积为60平方厘米,D、E分别为AB、AC边中点,求图中阴影部分面积?
如图,三角形ABC的面积为60平方厘米,D、E分别为AB、AC边中点,求图中阴影部分面积?分析:连接OA和DE,如下图由题意等底同高的三角形的面积相等可知△CAD和△ABE的面积都等于△ABC的一半,即60÷2=30(平方厘米),这两个△的面积都减去四边形的ADOE的面积得到S△BOD=S△COE,再根据等底同高的三角形的面积相等可知S△AOE=S△COE,S△AOD=S△BOD,所以S△AOE=S△COE=S△AOD,S△ADC=S△AOE+S△COE+S△AOD=30平方厘米,所以S△COE=30÷3=10平方厘米,由此可推出阴影部分的面积.
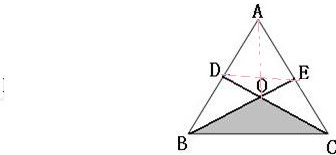

解答:解:由题意可知AE=CE,AD=BD,
根据等底同高的三角形的面积相等得:
S△ADC=S△BDC=60÷2=30平方厘米,S△AEB=S△CBE=30(平方厘米),
所以S△ADC=S△AEB=30(平方厘米),
则S△BOD=S△COE
再根据等底同高的三角形的面积相等得:
S△AOE=S△COE,S△AOD=S△BOD,
所以S△AOE=S△COE=S△AOD=S△BOD,
S△ADC=S△AOE+S△COE+S△AOD=30(平方厘米),
所以S△COE=30÷3=10(平方厘米),
所以图中阴影部分面积是30-10=20(平方厘米),
答:图中阴影部分面积是20平方厘米.
根据等底同高的三角形的面积相等得:
S△ADC=S△BDC=60÷2=30平方厘米,S△AEB=S△CBE=30(平方厘米),
所以S△ADC=S△AEB=30(平方厘米),
则S△BOD=S△COE
再根据等底同高的三角形的面积相等得:
S△AOE=S△COE,S△AOD=S△BOD,
所以S△AOE=S△COE=S△AOD=S△BOD,
S△ADC=S△AOE+S△COE+S△AOD=30(平方厘米),
所以S△COE=30÷3=10(平方厘米),
所以图中阴影部分面积是30-10=20(平方厘米),
答:图中阴影部分面积是20平方厘米.
点评:此题主要考查等底同高的三角形的面积相等和等量代换的知识,解决问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?
如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少? 如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=
如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD= 如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积=
如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积= 如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.
如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.