题目内容
在等式A×(B+C)=110+C中,A、B、C是3个互不相等的质数,那么A+B+C=
22
22
.分析:因为A,B,C是三个互不相同的质数,如果A、B、C全为奇,此时左端为偶,而右端为奇,所以A、B、C之中有一个为偶质数.A、B、C必有一个是2,其它的都是奇质数,所以C不能为偶,否则等式右端为偶,而左端为奇,另外,A不能为偶,如果A为偶,那么B、C为奇,此时等式左端为偶,而右端为奇,所以只能是B为偶质数了. 所以B=2,据此推导即可解答.
解答:解:Ax(B+C)=110+C,A,B,C是三个互不相同的质数.
A、B、C必有一个是2,否则它们都是奇数,偶质数只有唯一的一个,就是2,其它的都是奇质数,所以C不能为偶,否则等式右端为偶,而左端为奇,
另外,A、B、C全为奇,也不可能,此时左端为偶,而右端为奇,
所以A、B、C之中有一个为偶质数. A不能为偶,如果A为偶,那么B、C为奇,此时等式左端为偶,而右端为奇,所以只能是B为偶质数了. 所以B=2.
那么等式左边是偶数,右边是奇数,不可能.
同理A、C都不可能等于2,所以 B=2.
Ax(2+C)=110+C,
即 (A-1)x(C+2)=108,
108=4×27=12×9=2×54,讨论得 A=13,C=7.
所以 A+B+C=13+2+7=22.
故答案为:22.
A、B、C必有一个是2,否则它们都是奇数,偶质数只有唯一的一个,就是2,其它的都是奇质数,所以C不能为偶,否则等式右端为偶,而左端为奇,
另外,A、B、C全为奇,也不可能,此时左端为偶,而右端为奇,
所以A、B、C之中有一个为偶质数. A不能为偶,如果A为偶,那么B、C为奇,此时等式左端为偶,而右端为奇,所以只能是B为偶质数了. 所以B=2.
那么等式左边是偶数,右边是奇数,不可能.
同理A、C都不可能等于2,所以 B=2.
Ax(2+C)=110+C,
即 (A-1)x(C+2)=108,
108=4×27=12×9=2×54,讨论得 A=13,C=7.
所以 A+B+C=13+2+7=22.
故答案为:22.
点评:本题主要考查横式数字谜,解题关键是确定B的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .________.
.________.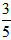 。
。