Question

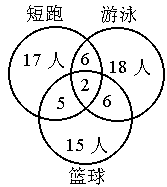
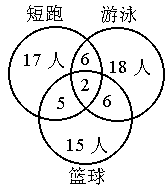
某个班的全体学生进行了短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优秀，其余每人至少有一个项目达到优秀，这部分学生达到优秀的项目、人数如下表：

短跑	游泳	篮球	短跑、游泳	游泳、篮球	篮球、短跑	短跑、游泳、篮球
17	18	15	6	6	5	2

求这个班的学生数．

Answer 1

分析：先用“文氏图法”画图把相交的部分表示出来，然后解答即可．

解答：解：先求至少有一个项目达到优秀的学生人数，看下面这个图：

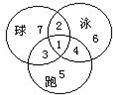
图中时三个圆圈分别代表短跑、游泳、篮球达到优秀的学生人数，其中的
“1”表示三个项目都优秀的人数，是：2；
“2”表示篮球、游泳达到优秀，但短跑没有达到优秀的人数，是：6-2=4；
“3”表示篮球、短跑达到优秀，但游泳没有达到优秀的人数，是：5-2=3；
“4”表示游泳、短跑达到优秀，但篮球没有达到优秀的学生数，是：6-2=4；
“5”表示只有短跑一项达到优秀的人数，是：17-（2+3+4）=8；
“6”表示只有游泳一项达到优秀的人数，是：18-（2+4+4）=8；
“7”表示只有篮球一项达到优秀的人数，是：15-（2+4+3）=6，
所以，只有一个项目达到优秀的人数是：2+4+3+4+8+8+6=35
还有4个人在三个项目上未达到优秀，所以全班学生数是35+4=39（人）
答：这个班有39名学生．

点评：本题还可以这样做：4+17+18+15中有两项达到优秀的学生被算了2次，应当从统计中去掉1次，成为4+17+18+15-6-6-5人，
但其中三项达到优秀的人，开始被算了3次，然后又被去掉3次，
所以还应将这部分人数加进来，即全班人数是：4+17+18+15-6-6-5+2=39（人）．