题目内容
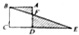 ABCD是正方形,△DEF的面积比△ABF的面积大6平方厘米,CD长4厘米,求DE的长度.
ABCD是正方形,△DEF的面积比△ABF的面积大6平方厘米,CD长4厘米,求DE的长度.
解:三角形BCE的面积为:4×4+6,
=16+6,
=22(平方厘米),
三角形BCE的底CE为:22×2÷4
=44÷4,
=11(厘米),
DE的长为:11-4=7(厘米).
答:DE的长为7厘米.
分析:根据题意,三角形DEF比三角形ABF面积大6平方厘米,那么三角形BCE的面积比正方形ABCD的面积大6平方厘米,可利用正方形的面积加上6平方厘米就是三角形的BCE的面积,再根据三角形的面积公式计算出底CE的长,DE=CE-CD,列式解答即可得到答案.
点评:解答此题的关键是确定三角形BCE的面积比正方形ABCD的面积小6平方厘米,然后再计算三角形BCE的底CE的长,最后再计算DE的长即可.
=16+6,
=22(平方厘米),
三角形BCE的底CE为:22×2÷4
=44÷4,
=11(厘米),
DE的长为:11-4=7(厘米).
答:DE的长为7厘米.
分析:根据题意,三角形DEF比三角形ABF面积大6平方厘米,那么三角形BCE的面积比正方形ABCD的面积大6平方厘米,可利用正方形的面积加上6平方厘米就是三角形的BCE的面积,再根据三角形的面积公式计算出底CE的长,DE=CE-CD,列式解答即可得到答案.
点评:解答此题的关键是确定三角形BCE的面积比正方形ABCD的面积小6平方厘米,然后再计算三角形BCE的底CE的长,最后再计算DE的长即可.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
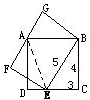 如图,四边形ABCD是正方形,边长是4厘米,四边形BEFG是长方形,长BE是5厘米,CE是3厘米,长方形BEFG的面积是
如图,四边形ABCD是正方形,边长是4厘米,四边形BEFG是长方形,长BE是5厘米,CE是3厘米,长方形BEFG的面积是 图中,三角形CDE的面积是140平方厘米,ABCD是正方形,CD:DE=5:4.求梯形ABCE的面积.
图中,三角形CDE的面积是140平方厘米,ABCD是正方形,CD:DE=5:4.求梯形ABCE的面积.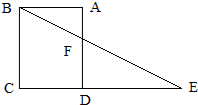
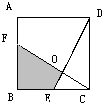 已知四边形ABCD是正方形,边长为3,BE=1.5,AF=1,求阴影部分的面积(如图).
已知四边形ABCD是正方形,边长为3,BE=1.5,AF=1,求阴影部分的面积(如图).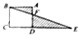 ABCD是正方形,△DEF的面积比△ABF的面积大6平方厘米,CD长4厘米,求DE的长度.
ABCD是正方形,△DEF的面积比△ABF的面积大6平方厘米,CD长4厘米,求DE的长度.