【题目】已知过点的曲线的方程为．

（Ⅰ）求曲线的标准方程:

（Ⅱ）已知点，为直线上任意一点，过作的垂线交曲线于点，．

（ⅰ）证明：平分线段（其中为坐标原点）；

（ⅱ）求最大值．

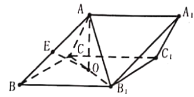
【题目】如图，三棱柱中，侧面为菱形，在侧面上的投影恰为的中点，为的中点．

（Ⅰ）证明：∥平面；

（Ⅱ）若，在线段上是否存在点（不与，重合）使得直线与平面成角的正弦值为若存在，求出的值；若不存在，说明理由．

（Ⅰ）写出频率分布直方图（高一）中的值；记高一、高二学生100人锻炼时间的样本的方差分别为，，试比较，的大小（只要求写出结论）；

（Ⅱ）估计在高一、高二学生中各随机抽取1人，恰有一人的锻炼时间大于20分钟的概率；

（Ⅲ）由频率分布直方图可以认为，高二学生锻炼时间服从正态分布．其中近似为样本平均数，近似为样本方差，且每名学生锻炼时间相互独立，设表示从高二学生中随机抽取10人，其锻炼时间位于的人数，求的数学期望．

注：①同一组数据用该区间的中点值作代表,计算得

②若，则，

【题目】PM2．5是衡量空气质量的重要指标，我国采用世卫组织的最宽值限定值，即PM2．5日均值在以下空气质量为一级，在空气质量为二级，超过为超标，如图是某地1月1日至10日的PM2．5（单位：）的日均值，则下列说法正确的是（ ）

A.10天中PM2．5日均值最低的是1月3日

B.从1日到6日PM2．5日均值逐渐升高

C.这10天中恰有5天空气质量不超标

D.这10天中PM2．5日均值的中位数是43

【题目】在直角坐标系中，已知点，，动点满足直线与的斜率之积为.记的轨迹为曲线.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

(1)求和的直角坐标方程；

(2)求上的点到距离的最小值.

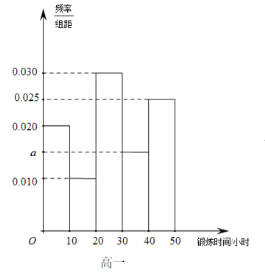
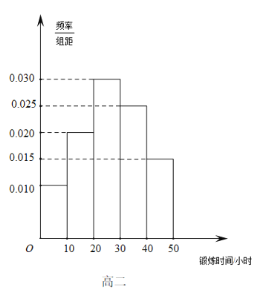
【题目】某中学高三(3)班有学生50人，现调查该班学生每周平均体育锻炼时间的情况，得到如下频率分布直方图，其中数据的分组区间为：，，，，，

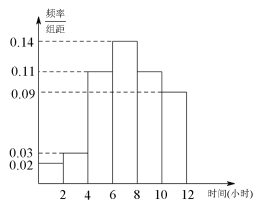
(1)从每周平均体育锻炼时间在的学生中，随机抽取2人进行调查，求这2人的每周平均体育锻炼时间都超过2小时的概率；

(2)已知全班学生中有40%是女姓，其中恰有3个女生的每周平均体育锻炼时间不超过4小时，若每周平均体育锻炼时间超过4小时称为经常锻炼，问：有没有90%的把握说明，经常锻炼与否与性别有关？

附：

【题目】PM2．5是衡量空气质量的重要指标，我国采用世卫组织的最宽值限定值，即PM2．5日均值在以下空气质量为一级，在空气质量为二级，超过为超标，如图是某地1月1日至10日的PM2．5（单位：）的日均值，则下列说法正确的是（ ）

A.10天中PM2．5日均值最低的是1月3日

B.从1日到6日PM2．5日均值逐渐升高

C.这10天中恰有5天空气质量不超标

D.这10天中PM2．5日均值的中位数是43

【题目】以直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的参数方程为（为参数）.

（1）求曲线的参数方程与直线的普通方程；

（2）设点过为曲线上的动点，点和点为直线上的点，且满足为等边三角形，求边长的取值范围.

【题目】已知函数.

（1）讨论函数在上的单调性；

（2）是否存在正实数，使与的图象有唯一一条公切线，若存在，求出的值，若不存在，请说明理由.

【题目】已知点，点在轴负半轴上，以为边做菱形，且菱形对角线的交点在轴上，设点的轨迹为曲线.

（1）求曲线的方程；

（2）过点，其中，作曲线的切线，设切点为，求面积的取值范围.