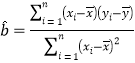（1）应收集多少位女生的样本数据？

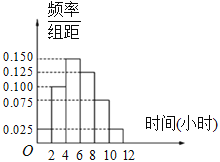
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据分组区间为：，试估计该校学生每周平均体育运动时间超过4小时的概率.

（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表，并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关？

附：，其中.

【题目】如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．

（1）证明：EF∥BC；
（2）若AG等于⊙O的半径，且AE=MN=2 ，求四边形EBCF的面积．

【题目】已知 是（﹣∞，+∞）上的增函数，那么a的取值范围是（ ）
A.[ ，3）
B.（0，3）
C.（1，3）
D.（1，+∞）

【题目】已知函数f（x）=ax3+bx+c在点x=2处取得极值c﹣16．
（1）求a，b的值；
（2）若f（x）有极大值28，求f（x）在[﹣3，3]上的最小值．

【题目】已知是椭圆的左、右焦点，为坐标原点，点在椭圆上，线段与轴的交点为，且．

（1）求椭圆的标准方程；

（2）圆是以为直径的圆，直线与圆相切，并与椭圆交于不同的两点，，当，且满足时，求的面积的取值范围．

请考生在第22、23两题中任选一题作答．注意：只能做所选定的题目.如果多做，则按所做的第一个题目计分．

【题目】已知函数f（x）=log2x，x∈（4，8），则函数y=f（x2）+ 的值域为（ ）
A.[8，10）
B.（ ，10）
C.（8， ）
D.（ ，10）

【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标，它是指空气净化器从开始使用到净化效率为时对颗粒物的累计净化量(单位：克)．根据国家标准，对空气净化器的累计净化量(CCM)有如下等级划分：

已知某批空气净化器共台，其累计净化量都分布在区间内，为了解其质量，随机抽取了台净化器作为样本进行估计，按照，，，，均匀分组，其中累计净化量在的所有数据有：，，，，和，并绘制了如下频率分布直方图．

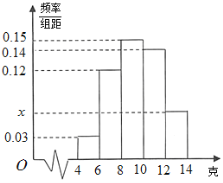
（1）求的值及频率分布直方图中的值；

（2）以样本估计总体，试估计这批空气净化器（共2000台）中等级为的空气净化器有多少台？

（3）从累计净化量在的样本中随机抽取2台，求恰好有1台等级为的概率．

（Ⅰ）从这5年中随机抽取两年，求外出旅游的家庭数至少有1年多于20个的概率；

（Ⅱ）利用所给数据，求出春节期间外出旅游的家庭数与年份之间的回归直线方程，判断它们之间是正相关还是负相关；并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.

参考公式：，

【题目】已知双曲线C： （a＞0，b＞0）过点A（1，0），且离心率为
（1）求双曲线C的方程；
（2）已知直线x﹣y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值．

【题目】下列函数中，既是偶函数，又在区间上单调递减的是

A． B．

C． D．