摘要：(3)设直线与抛物线交于点E.F.与轴交于点M,抛物线与轴交于点N．若抛物线的对称轴为直线.△MNE与△MNF的面积之比为5:1.试判断△ABC的形状.并证明你的结论．

网址：http://m.1010jiajiao.com/timu_id_765116[举报]

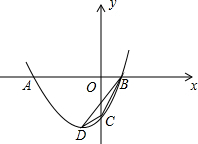抛物线y=ax²+bx+c（a＞0）经过点A（-3

，0）与y轴交于点C，设抛物线的顶点为D，在△BCD中，边CD的高为h．
（1）若c=ka，求系数k的值；
（2）当∠ACB=90°，求a及h的值；
（3）当∠ACB≥90°时，经过探究、猜想请你直接写出h的取值范围．
（不要求书写探究、猜想的过程）查看习题详情和答案>>

）x+（k+1）（k为常数）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜0＜x₂）两点，与y轴交于C点，且满足（OA+OB）²=OC²+16．
（1）求此抛物线的解析式；
（2）设M、N是抛物线在x轴上方的两点，且到x轴的距离均为1，点P是抛物线的顶点，问：过M、N、C三点的圆与直线CP是否只有一个公共点C？试证明你的结论．查看习题详情和答案>>

抛物线y= $数学公式$ x²+（k+ $数学公式$ ）x+（k+1）（k为常数）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜0＜x₂）两点，与y轴交于C点，且满足（OA+OB）²=OC²+16．
（1）求此抛物线的解析式；
（2）设M、N是抛物线在x轴上方的两点，且到x轴的距离均为1，点P是抛物线的顶点，问：过M、N、C三点的圆与直线CP是否只有一个公共点C？试证明你的结论．

查看习题详情和答案>>

抛物线y=ax² +bx+c的顶点为P，与x轴的两个交点为M、N(点M在点N的左侧)，△PMN的三个内角么∠P、∠M、∠N所对的边分别为p、m、n，且m =n，若关于x的方程(p -m) x²+2nx+(p+m)=0有两个相等的实数根．
(1)试判断△PMN的形状；
(2)当顶点P的坐标为（2，-1）时，求抛物线的解析式；
(3)设抛物线与了轴的交点为Q.
求证：直线y=x-1将四边形MPNQ分成的两个图形的面积相等．

查看习题详情和答案>>

直线与轴相交于点，连结，抛物线从点沿方向平移，与直线交于点，顶点到点时停止移动．

（1）求线段所在直线的函数解析式；（2）设抛物线顶点的横坐标为,①用的代数式表示点的坐标；②当为何值时，线段最短；

（3）当线段最短时，相应的抛物线上是否存在点，使△ 的面积与△的面积相等，若存在，请求出点的坐标；若，不存在，请说明理由．

查看习题详情和答案>>