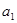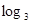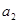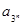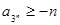摘要：知|PM|>|PN|,故P为双曲线右支上的点.所以|PM|=|PN|+2. ②将②代入①.得2||PN|2-|PN|-2=0.解得|PN|=,所以|PN|=.因为双曲线的离心率e==2,直线l:x=是双曲线的右准线.故=e=2,所以d=|PN|,因此解法:设P(x,y).因|PN|1知|PM|=2|PN|22|PN|>|PN|,
网址：http://m.1010jiajiao.com/timu_id_75517[举报]
已知函数
(
>0)，过点P(1，0)作曲线
的两条切线PM、PN，为M、N．
(1)当t=2时，求函数
的单调递增区间；
(2)设|MN|=g(t)，求函数g(t)的表达式；
(3)在(2)的条件下，若对任意正整数
，在区间[2，+
]内总存在
+1个实数
、
、…、
、
，使得不等式g()+g()+…+g()<g()成立，求的最大值．
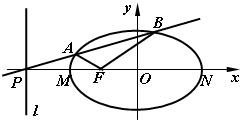如图，设F是椭圆
1常数，求函数
定义
上单调递增；命题Q：不等式
对任意实数
恒成立；若
是真命题，求实数
的取值范
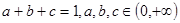,求证：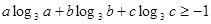
;
，
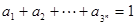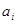>0(i=1,2,3,…,3n)，求证：
