摘要:8(1)小亮发现.课桌高y是课桌凳高x的一次函数.请你求出它们的函数关系式,
网址:http://m.1010jiajiao.com/timu_id_750059[举报]
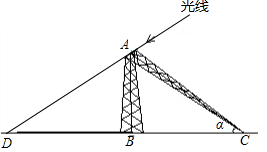 雨过天晴的一个下午,小明和小亮发现路边从A处折断的一根电线杆,他们测量发现折断部分AC与地面的夹角α=30°,树身部分AB在某时刻阳光下的BD=6米,而在同一时刻,身高1.6米的小亮的影子是2.4米,求树原来的高度.
雨过天晴的一个下午,小明和小亮发现路边从A处折断的一根电线杆,他们测量发现折断部分AC与地面的夹角α=30°,树身部分AB在某时刻阳光下的BD=6米,而在同一时刻,身高1.6米的小亮的影子是2.4米,求树原来的高度. (2012•浦口区一模)提出问题:
(2012•浦口区一模)提出问题:如图,在△ABC中,∠A=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接EG,小亮发现△ABC与△AEG面积相等.小亮思考:这个问题中,如果∠A≠90°,那么△ABC与△AEG面积是否仍然相等?
猜想结论:
经过研究,小亮认为:上述问题中,对于任意△ABC,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,那么△ABC与△AEG面积相等.
证明猜想:
(1)请你帮助小亮画出图形,并完成证明过程.已知:以△ABC的两边AB、AC为边长分别向外作正方形
 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.结论应用:
(2)学校教学楼前的一个六边形花圃被分成七个部分,分别种上不同品种的花卉,其中四边形ABCD、CIHG、GFED均为正方形,且面积分别为9m2、5m2和4m2.求这个六边形花圃ABIHFE的面积.
已知△AOB,将△AOB绕O点旋转到△COD位置,使C点落在OB边上,连接AC、BD.
(1)若∠AOB=90°(如图1),小亮发现∠BAC=∠BDC,请你证明这个结论;
(2)若∠AOB=60°(如图2),小亮发现的结论是否仍然成立?说明理由;
(3)若∠AOB为任意角α(如图3),小亮发现的结论还成立吗?说明理由;

查看习题详情和答案>>
(1)若∠AOB=90°(如图1),小亮发现∠BAC=∠BDC,请你证明这个结论;
(2)若∠AOB=60°(如图2),小亮发现的结论是否仍然成立?说明理由;
(3)若∠AOB为任意角α(如图3),小亮发现的结论还成立吗?说明理由;

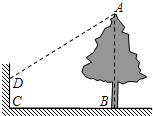 小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.
小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.