(1)过点P作直线PQ∥CD.交AB于点Q,(2)过点P作垂线段PR⊥CD.垂足为R,(3)若∠DCB=120°.猜想∠PQC是多少度?请说明理由.——青夏教育精英家教网——

摘要：(1)过点P作直线PQ∥CD.交AB于点Q,(2)过点P作垂线段PR⊥CD.垂足为R,(3)若∠DCB=120°.猜想∠PQC是多少度?请说明理由.

网址：http://m.1010jiajiao.com/timu_id_748642[举报]

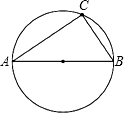如图，AB为圆O的直径，在圆O上取异于A、B的一点C，并连接BC、AC．若想在直径AB上取一点P，使得P与直线BC的距离等于AP长，判断下列四个作法何者正确？（　　）

的中垂线，交AB于P点

B、作∠ACB的角平分线，交AB于P点

C、作∠ABC的角平分线，交

于D点，过D作直线BC平行线，交AB于P点

D、过A作圆O的切线，交直线BC于D点，作∠ADC的角平分线，交AB于P点

查看习题详情和答案>>

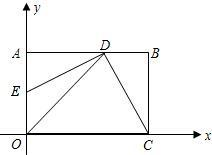已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．
（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为

，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．查看习题详情和答案>>

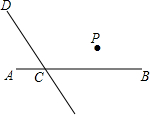如图，直线CD与直线AB相交于点C，根据下列语句画图、解答．
（1）过点P作PQ∥CD，交AB于点Q；
（2）过点P作PR⊥CD，交AB于点O，垂足于CD为R；
（3）若∠DCB=120°，猜想∠POC是多少度？并说明理由．

查看习题详情和答案>>

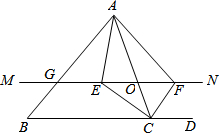如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，交AB于点G，设MN交∠BCA的平分线于点E，交∠ACD的角平分线于点F．
（1）求证：OE=OF；
（2）若△ABC是以AB为斜边的直角三角形，猜想并证明当点O运动到何处时四边形AECF为正方形？此时，如果AE=

，AB=4，求sin∠BAE的值．

查看习题详情和答案>>

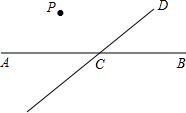如图，直线CD与直线AB相交于C，根据下列语句画图
（1）过点P作PQ∥CD，交AB于点Q．
（2）过点P作PR⊥CD，垂足为R．

查看习题详情和答案>>