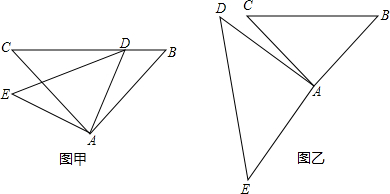
摘要:“如图甲.已知.在△ABC中.AB=AC.P是△ABC内任意一点.将AP绕点A顺时针旋转至AQ.使∠QAP=∠BAC.连结BQ.CP.则BQ=CP. 小亮是个爱动脑筋的同学.他通过对图甲的分析.证明了△ABQ≌△ACP.从而证得BQ=CP.之后.他将点P移到等腰三角形ABC之外.原题中其他条件不变.发现“BQ=CP 仍然成立.请你就图乙给出证明.
网址:http://m.1010jiajiao.com/timu_id_741179[举报]
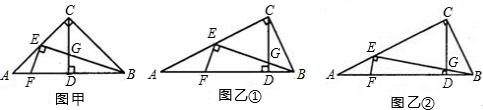
已知:在△ABC中,AB=AC,将△ABC沿BD折叠,使点A落在BC边(或延长线)上的点E处,若∠A=90°时(如图甲),易证:DE+CD+CE=BC.
当∠A>90°时(如图乙),上述结论是否还成立?若成立,请给予证明;若不成立,请你猜想线段DE、CD、CE、BC 之间的数量关系,并证明你的猜想;
当∠A<90°时(如图丙),线段DE、CD、CE、BC之间的又有怎样的数量关系?请写出你的猜想,不需证明.
查看习题详情和答案>>
当∠A>90°时(如图乙),上述结论是否还成立?若成立,请给予证明;若不成立,请你猜想线段DE、CD、CE、BC 之间的数量关系,并证明你的猜想;
当∠A<90°时(如图丙),线段DE、CD、CE、BC之间的又有怎样的数量关系?请写出你的猜想,不需证明.

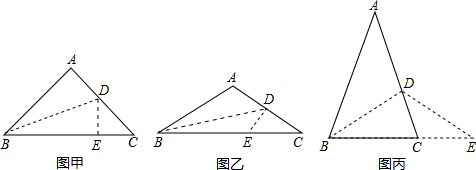
已知:在△ABC中,AB=AC,将△ABC沿BD折叠,使点A落在BC边(或延长线)上的点E处,若∠A=90°时(如图甲),易证:DE+CD+CE=BC.
当∠A>90°时(如图乙),上述结论是否还成立?若成立,请给予证明;若不成立,请你猜想线段DE、CD、CE、BC 之间的数量关系,并证明你的猜想;
当∠A<90°时(如图丙),线段DE、CD、CE、BC之间的又有怎样的数量关系?请写出你的猜想,不需证明.
查看习题详情和答案>>
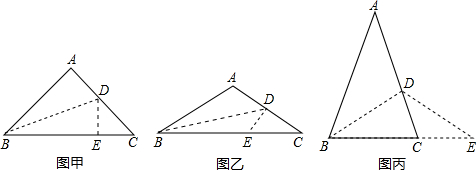
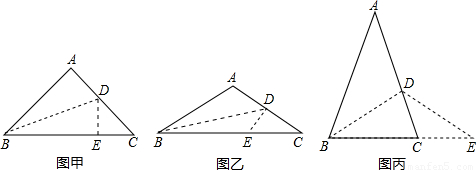
已知:在△ABC中,AB=AC,将△ABC沿BD折叠,使点A落在BC边(或延长线)上的点E处,若∠A=90°时(如图甲),易证:DE+CD+CE=BC.
当∠A>90°时(如图乙),上述结论是否还成立?若成立,请给予证明;若不成立,请你猜想线段DE、CD、CE、BC 之间的数量关系,并证明你的猜想;
当∠A<90°时(如图丙),线段DE、CD、CE、BC之间的又有怎样的数量关系?请写出你的猜想,不需证明.
查看习题详情和答案>>
当∠A>90°时(如图乙),上述结论是否还成立?若成立,请给予证明;若不成立,请你猜想线段DE、CD、CE、BC 之间的数量关系,并证明你的猜想;
当∠A<90°时(如图丙),线段DE、CD、CE、BC之间的又有怎样的数量关系?请写出你的猜想,不需证明.

查看习题详情和答案>>