摘要：18．在△ABC中.AB=AC=5..如果圆O的半径为.且经过点B.C.那么线段AO的长等于 .
网址：http://m.1010jiajiao.com/timu_id_741080[举报]
数学课上，老师出示了如下框中的题目，
小敏与同桌小聪讨论后，进行了如下解答：
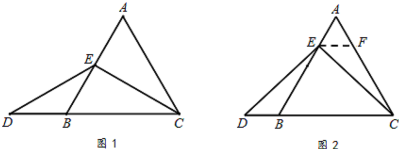
（1 ）特殊情况探索结
论当点E为AB的中点时，如图1 ，确定线段AE与DB的大小关系，请你直接写出结论：AE( )DB （填“＞”，“＜”或“=”）．
（2 ）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE( )DB （填
“＞”，“＜“=”），理由如下：如图2，过点E作EF∥BC，交AC于点F。（请你完成以下解答过程）
（3 ）拓展结论，设计新题
在等边三角形ABC中，点E 在直线AB上，点D 在直线BC上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长。（请你直接写出结果）
（1 ）特殊情况探索结
论当点E为AB的中点时，如图1 ，确定线段AE与DB的大小关系，请你直接写出结论：AE( )DB （填“＞”，“＜”或“=”）．（2 ）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE( )DB （填
“＞”，“＜“=”），理由如下：如图2，过点E作EF∥BC，交AC于点F。（请你完成以下解答过程）（3 ）拓展结论，设计新题
在等边三角形ABC中，点E 在直线AB上，点D 在直线BC上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长。（请你直接写出结果）
数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图，试确定线段AE与DB的大小关系，并说明理由”，小敏与同桌小聪讨论后，进行了如下解答：
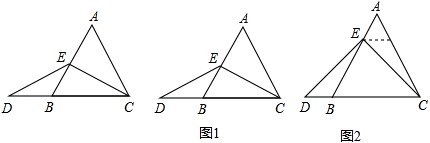
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE______DB（填“＞”，“＜”或“=”）；
（2）特例启发，解答题目解：
题目中，AE与DB的大小关系是：AE_______DB（填“＞”，“＜”或“=”），理由如下：如图2，过点E作EF∥BC，交AC于点F。（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）。
查看习题详情和答案>>
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE______DB（填“＞”，“＜”或“=”）；
（2）特例启发，解答题目解：
题目中，AE与DB的大小关系是：AE_______DB（填“＞”，“＜”或“=”），理由如下：如图2，过点E作EF∥BC，交AC于点F。（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）。
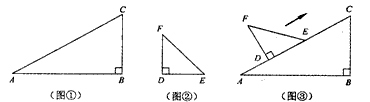
刘扬同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、 ②．图①中，∠B=90°，∠A=30°，BC=6cm；图②中，∠D=90°，∠E=45°，DE=4 cm．图③是刘扬同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上（移动开始时点D 与点A重合）．
（1）在△DEF沿AC方向移动的过程中，刘扬同学发现：F、C两点间的距离逐渐______。（填“不变”、“变大”或“变小”）
（2）刘扬同学经过进一步地研究，编制了如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行?
问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD=15°？如果存在，求出AD的长度；如果不存在，请说明理由． 请你分别完成上述三个问题的解答过程．
（1）在△DEF沿AC方向移动的过程中，刘扬同学发现：F、C两点间的距离逐渐______。（填“不变”、“变大”或“变小”）
（2）刘扬同学经过进一步地研究，编制了如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行?
问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD=15°？如果存在，求出AD的长度；如果不存在，请说明理由． 请你分别完成上述三个问题的解答过程．
阅读以下短文，然后解决下列问题：
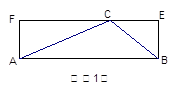
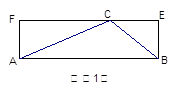
如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”。如图（1）所示，矩形ABEF即为△ABC的“友好矩形”。显然，当△ABC是钝角三角形时，其“友好矩形”只有一个。
1.仿照以上叙述，说明什么是一个三角形的“友好平行四边形”
2.如图（2），若△ABC为直角三角形，且∠C=90°，在图（2）
中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；
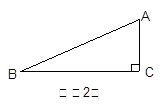
3.若△ABC是锐角三角形，且BC>AC>AB，在图（3）中画出△ABC的所有“友好矩形”，指出其中周长最大的矩形。（标上字母）
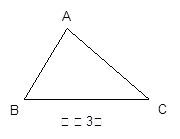
查看习题详情和答案>>
阅读以下短文，然后解决下列问题：
如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”。如图（1）所示，矩形ABEF即为△ABC的“友好矩形”。显然，当△ABC是钝角三角形时，其“友好矩形”只有一个。
【小题1】仿照以上叙述，说明什么是一个三角形的“友好平行四边形”
【小题2】如图（2），若△ABC为直角三角形，且∠C=90°，在图（2）
中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；
【小题3】若△ABC是锐角三角形，且BC>AC>AB，在图（3）中画出△ABC的所有“友好矩形”，指出其中周长最大的矩形。（标上字母）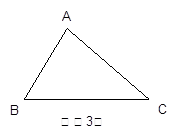
查看习题详情和答案>>
如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”。如图（1）所示，矩形ABEF即为△ABC的“友好矩形”。显然，当△ABC是钝角三角形时，其“友好矩形”只有一个。
【小题1】仿照以上叙述，说明什么是一个三角形的“友好平行四边形”
【小题2】如图（2），若△ABC为直角三角形，且∠C=90°，在图（2）
中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；
【小题3】若△ABC是锐角三角形，且BC>AC>AB，在图（3）中画出△ABC的所有“友好矩形”，指出其中周长最大的矩形。（标上字母）
查看习题详情和答案>>