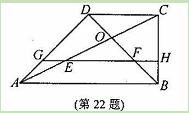
摘要:20.在梯形ABCD中.AB∥CD.∠A=90°. AB=2.BC=3.CD=1.E是AD中点. 求证:CE⊥BE.
网址:http://m.1010jiajiao.com/timu_id_725614[举报]
(本题满分10分)如图,梯形ABCD中,AD∥BC,CE⊥AB于E, BF⊥CD于F,连接AF、DE.
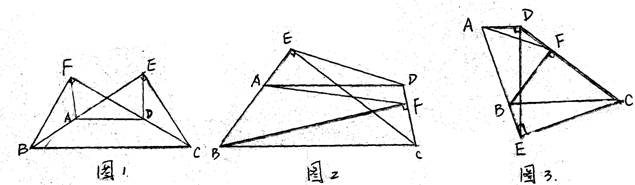
1.(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
2.(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
3.(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA=
查看习题详情和答案>>
(本题满分10分)如图,梯形ABCD中,AD∥BC,CE⊥AB于E,BF⊥CD于F,连接AF、DE.

小题1:(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
小题2:(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
小题3:(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA=

小题1:(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
小题2:(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
小题3:(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA=
(本题满分10分)如图,梯形ABCD中,AD∥BC,CE⊥AB于E, BF⊥CD于F,连接AF、DE.

1.(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
2.(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
3.(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA=
查看习题详情和答案>>
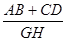 的值。
的值。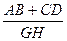 的值。
的值。