摘要:9.如图所示.其中与下图图案全相同的是
网址:http://m.1010jiajiao.com/timu_id_684701[举报]
某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪)。
(1)请你根据这一问题,在每种方案中都列出方程,并任选其一求出设计方案中道路的宽为多少米?(精确到0.1米)
①甲方案设计图纸为图l,设计草坪的总面积为600平方米。
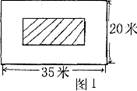
②乙方案设计图纸为图2,设计草坪的总面积为600平方米。
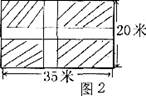
③丙方案设计图纸为图3,设计草坪的总面积为540平方米。
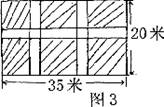
(2)请你也按上述要求画出自己的一种设计方案,列出方程,不求解。
查看习题详情和答案>>
在数学活动课上,老师要求同学们先做下面的“循环分割”操作,然后再探索规律:
如图1,是一等腰梯形纸片,其腰长与上底长相等,且底角分别60°和120°,按要求开始操作(每次分割,纸片均不得留有剩余);

第1次分割:将原等腰梯形纸片分割成3个等边三角形;
第2次分割:将上次分割出的一个等边三角形分割成3个全等的等腰梯形,然后将刚分割出的一个等腰梯形分割成3个等边三角形;
以后按第2次分割的方法进行下去…请解答下列问题:
(1)请你在图2中画出前两次分割后的图案;
(2)若原等腰梯形的面积为a,请你通过操作、观察,将第2次,第3次分割后所得的一个最小等边三角形的面积分别填入下表:
(3)请你猜想,分割所得的一个最小等边三角形面积S与分割次数n有何关系?(请直接用含a的式子表示,不需写推理过程)
查看习题详情和答案>>
如图1,是一等腰梯形纸片,其腰长与上底长相等,且底角分别60°和120°,按要求开始操作(每次分割,纸片均不得留有剩余);

第1次分割:将原等腰梯形纸片分割成3个等边三角形;
第2次分割:将上次分割出的一个等边三角形分割成3个全等的等腰梯形,然后将刚分割出的一个等腰梯形分割成3个等边三角形;
以后按第2次分割的方法进行下去…请解答下列问题:
(1)请你在图2中画出前两次分割后的图案;
(2)若原等腰梯形的面积为a,请你通过操作、观察,将第2次,第3次分割后所得的一个最小等边三角形的面积分别填入下表:
| 分割次数(n) | 1 | 2 | 3 | … | ||
| 一个最小等边三角形的面积(S) |
|
… |
在数学活动课上,老师要求同学们先做下面的“循环分割”操作,然后再探索规律:
如图1,是一等腰梯形纸片,其腰长与上底长相等,且底角分别60°和120°,按要求开始操作(每次分割,纸片均不得留有剩余);

第1次分割:将原等腰梯形纸片分割成3个等边三角形;
第2次分割:将上次分割出的一个等边三角形分割成3个全等的等腰梯形,然后将刚分割出的一个等腰梯形分割成3个等边三角形;
以后按第2次分割的方法进行下去…请解答下列问题:
(1)请你在图2中画出前两次分割后的图案;
(2)若原等腰梯形的面积为a,请你通过操作、观察,将第2次,第3次分割后所得的一个最小等边三角形的面积分别填入下表:
| 分割次数(n) | 1 | 2 | 3 | … |
| 一个最小等边三角形的面积(S) |  a a | … |
1.从不同角度计算图中边长为c的正方形的面积,你得到了什么?发现了什么?与勾股定理有关吗?试试看.
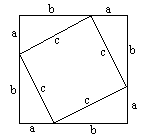
2.观察勾股定理a2+b2=c2中的c2、a2和b2,你想到了什么?
3.利用上图中四个完全相同的直角三角形,你还能拼出与c2有关的图形吗?能利用这个图形验证勾股定理吗?
4.用上图中的四个完全相同的直角三角形可以拼成如图Ⅰ所示的图形,这个图形被称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.观察图Ⅰ,你能验证c2=a2+b2吗?把你的验证过程写下来,并与同伴进行交流.

2002年世界数学家大会(ICM-2002)在北京召开.图Ⅱ是此届大会的会标,其中央图案正是经过艺术处理的“弦图”.它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎来自世界各地的数学家们.
