网址:http://m.1010jiajiao.com/timu_id_61509[举报]
一、 填空题(48分)
1、4 2、(理)20(文) 3、
3、 4、
4、 5、
5、 6、
6、 7、(理)
7、(理) (文)4 8、6 9、
(文)4 8、6 9、 10、
10、 11、如
11、如 12、
12、
二、 选择题(16分)
13、B 14、B 15、C 16、A
三、 解答题(86分)
17、(12分)(1) ,则
,则 ……………………… (6分)
……………………… (6分)
(2) ………………………………………(9分)
………………………………………(9分)

 …………………………………………………………(12分)
…………………………………………………………(12分)
18、(12分)(1)它是有一条侧棱垂直于底面的四棱锥

…………………………………………………………(6分)
(注:评分注意实线、虚线;垂直关系;长度比例等)
(2)由题意, ,则
,则 ,
,
 ,
,
∴需要3个这样的几何体可以拼成一个棱长为6的正方体 …(12分)
…(12分)
19、(14分)
(1)抛物线的焦点为(1,0) ……………………………………………………(2分)
设椭圆方程为 ,则
,则
∴椭圆方程为 ……………………………………………(6分)
……………………………………………(6分)
(2)设 ,则
,则

 ………………(8分)
………………(8分)
① 当 时,
时, ,即
,即 时,
时, ;
;
② 当 时,
时, ,即
,即 时,
时, ;
;
综上, 。……………………………………(14分)
。……………………………………(14分)
(注:也可设 解答,参照以上解答相应评分)
解答,参照以上解答相应评分)
20、(14分)
(1)设当天的旅游收入为L,由 得
得
 ……………………………(2分)
……………………………(2分)
由 ,知
,知 …………………………………………(4分)
…………………………………………(4分)
 ,
, 得
得 。
。
即当天的旅游收入是20万到60万。……………………………………………(7分)
(2)则每天的旅游收入上缴税收后不低于220000元
由 (
( )得
)得 ;
;
由 (
( )得
)得 ;
;
∴ ………………………………………………………………………(11分)
………………………………………………………………………(11分)
代入可得 ∴
∴
即每天游客应不少于1540人。……………………………………………………(14分)
21、(16分)
(1) 由 ,得
,得 则
则 故
故 (4分)
(4分)
(2) 由 ,得
,得 即
即
∴ ,所以
,所以 是不唯一的。……………………………………(10分)
是不唯一的。……………………………………(10分)
(3) ,
, ,
, ;
;
∴ …………………………………………(12分)
…………………………………………(12分)
(文)………………………………………………………………………………(16分)
(理)一般地,对任意复数 ,有
,有 。
。
证明:设 ,
,

 ,
,

∴ 。…………………………………………………(16分)
。…………………………………………………(16分)
22、(18分)
(1) ………………………………………………………………(6分)
………………………………………………………………(6分)
(2)由 解得
解得
即
解得 …………………………………(12分)
…………………………………(12分)
(3) 由 ,
,
又 ,
,
当 时,
时, ,
, ,
,
∴对于 时,
时, ,命题成立。………………(14分)
,命题成立。………………(14分)
以下用数学归纳法证明 对
对 ,且
,且 时,都有
时,都有 成立
成立
假设 时命题成立,即
时命题成立,即 ,
,
那么 即
即 时,命题也成立。
时,命题也成立。
∴存在满足条件的区间 。………………………………(18分)
。………………………………(18分)
设 ,
, 是椭圆
是椭圆
 上的两点,已知向量m
上的两点,已知向量m ,n
,n ,若m
,若m n
n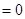 且椭圆的离心率
且椭圆的离心率 ,短轴长为2,
,短轴长为2, 为坐标原点。
为坐标原点。
(1)求椭圆的方程;
(2)试问: 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由。
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由。
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| 2 |
| AF2 |
| F1F2 |
| 1 |
| 3 |
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|MQ|=2|QF|,求直线l的斜率. 查看习题详情和答案>>
| x | 3 | -2 | 4 |
|
| ||||||||
| y | -2
|
0 | -4 |
|
-
|
(2)设直线l与椭圆C1交于不同两点M、N,且
| OM |
| ON |