摘要:设圆上任意一点为P,在三角形POM中.由余弦定理:PM2=OM2+OP2-2OM.OPcos∠POM故方程为ρ2-2ρ0ρcos(θ-θ0)+ρ02-r2=0(2)思考特殊位置的圆①圆心在极点时:ρ=r②圆心为(r,0)时:ρ=2rcosθ
网址:http://m.1010jiajiao.com/timu_id_569656[举报]
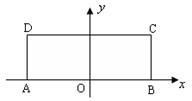
(本小题满分14分)已知长方形 ,
,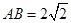 ,
,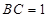 ,以
,以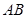 的中点
的中点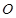 为
为
原点建立如图所示的平面直角坐标系 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中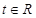 ,探究
,探究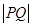 的最
的最
小值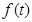 。
。
查看习题详情和答案>>
在平面直角坐标系xOy中,已知圆x2+y2=1与x轴正半轴的交点为F,AB为该圆的一条弦,直线AB的方程为x=m.记以AB为直径的圆为⊙C,记以点F为右焦点、短半轴长为b(b>0,b为常数)的椭圆为D.
(1)求⊙C和椭圆D的标准方程;
(2)当b=1时,求证:椭圆D上任意一点都不在⊙C的内部;
(3)已知点M是椭圆D的长轴上异于顶点的任意一点,过点M且与x轴不垂直的直线交椭圆D于P、Q两点(点P在x轴上方),点P关于x轴的对称点为N,设直线QN交x轴于点L,试判断
•
是否为定值?并证明你的结论.
查看习题详情和答案>>
(1)求⊙C和椭圆D的标准方程;
(2)当b=1时,求证:椭圆D上任意一点都不在⊙C的内部;
(3)已知点M是椭圆D的长轴上异于顶点的任意一点,过点M且与x轴不垂直的直线交椭圆D于P、Q两点(点P在x轴上方),点P关于x轴的对称点为N,设直线QN交x轴于点L,试判断
| OM |
| OL |
在直角坐标坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P向y轴作垂线段PP′,P′为垂足.
(1)求线段PP′中点M的轨迹C的方程.
(2)过点Q(一2,0)作直线l与曲线C交于A、B两点,设N是过点(-
,0),且以言
=(0,1)为方向向量的直线上一动点,满足
=
+
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线Z的方程;若不存在,说明理由.
查看习题详情和答案>>
(1)求线段PP′中点M的轨迹C的方程.
(2)过点Q(一2,0)作直线l与曲线C交于A、B两点,设N是过点(-
| 4 |
| 17 |
| a |
| ON |
| OA |
| OB |
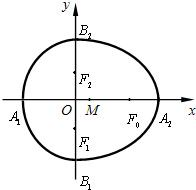 我们把由半椭圆
我们把由半椭圆