摘要:思考:1.一般地.ρ可以为负的情况下.点还可以表示成什么形式?或
网址:http://m.1010jiajiao.com/timu_id_569582[举报]
对于数列{an},规定数列{△an}为数列{an}的一阶差分数列,其中△an=an+1-an(n∈N*);一般地,规定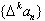 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中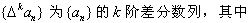
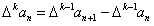 ,且
,且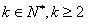 。
。
(1)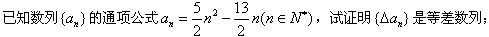
(2)若数列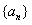 的首项
的首项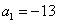 ,且满足
,且满足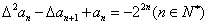 ,求数列
,求数列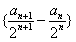 及
及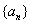 的通项公式;
的通项公式;
(3)在(2)的条件下,判断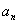 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。
查看习题详情和答案>>
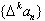 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中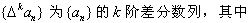
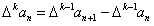 ,且
,且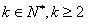 。
。(1)
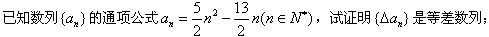
(2)若数列
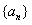 的首项
的首项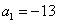 ,且满足
,且满足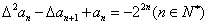 ,求数列
,求数列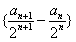 及
及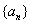 的通项公式;
的通项公式; 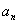 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。 拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
倍”,请你写出此命题在立体几何中类似的真命题:
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
.(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
| ||
| 2 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
| ||
| 3 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
.
| ||
| 3 |
在三棱柱ABC-A1B1C1中,各棱长都等于2a,下底面ABC在水平面上保持不动,在侧棱与底面所成的角保持为60°的情况下,上底面A1B1C1还是可以移动的,则△A1B1C1在下底面ABC所在平面上的竖直投影所扫过的区域的面积为
查看习题详情和答案>>
(6+
+π)a2
| 3 |
(6+
+π)a2
.| 3 |