摘要：解:→==.变换矩阵为
网址：http://m.1010jiajiao.com/timu_id_569400[举报]
（1）已知矩阵M
所对应的线性变换把点A（x，y）变成点A′（13，5），试求M的逆矩阵及点A的坐标．
（2）已知直线l：3x+4y-12=0与圆C：
（θ为参数 ）试判断他们的公共点个数；
（3）解不等式|2x-1|＜|x|+1． 查看习题详情和答案>>
|
（2）已知直线l：3x+4y-12=0与圆C：
|
（3）解不等式|2x-1|＜|x|+1． 查看习题详情和答案>>
选修4-2：矩阵及其变换（1）如图，向量
| OA |
| OB |
| OA′ |
| OB′ |
（Ⅰ）求矩阵M；
（Ⅱ）并求y=sin(x+
| π |
| 3 |
选修4-4：坐标系与参数方程
（ 2）在直角坐标系x0y中，直线l的参数方程为
|
| 5 |
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于点A，B．若点P的坐标为（3，
| 5 |
选修4-5：不等式选讲
（3）已知x，y，z为正实数，且
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
选修4-2：矩阵及其变换
（1）如图，向量
被矩阵M作用后分别变成
，
（Ⅰ）求矩阵M；
（Ⅱ）并求
在M作用后的函数解析式；
选修4-4：坐标系与参数方程
（ 2）在直角坐标系x0y中，直线l的参数方程为
（t为参数），在极坐标系（与直角坐标系x0y取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于点A，B．若点P的坐标为（3，
），求|PA|+|PB|．
选修4-5：不等式选讲
（3）已知x，y，z为正实数，且
，求x+4y+9z的最小值及取得最小值时x，y，z的值．
查看习题详情和答案>>
（1）如图，向量
被矩阵M作用后分别变成，（Ⅰ）求矩阵M；
（Ⅱ）并求
在M作用后的函数解析式；选修4-4：坐标系与参数方程
（ 2）在直角坐标系x0y中，直线l的参数方程为
（t为参数），在极坐标系（与直角坐标系x0y取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为．（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于点A，B．若点P的坐标为（3，
），求|PA|+|PB|．选修4-5：不等式选讲
（3）已知x，y，z为正实数，且
，求x+4y+9z的最小值及取得最小值时x，y，z的值．
查看习题详情和答案>>
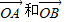被矩阵M作用后分别变成
，
在M作用后的函数解析式；
（t为参数），在极坐标系（与直角坐标系x0y取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
），求|PA|+|PB|．
，求x+4y+9z的最小值及取得最小值时x，y，z的值．
所对应的线性变换把点A（x，y）变成点A′（13，5），试求M的逆矩阵及点A的坐标．
（θ为参数 ）试判断他们的公共点个数；