摘要:解:设(x0,y0)为已知椭圆上任意一点.在作用下变为点(x,y) ==.于是x=0,y=y0,由于(x0,y0)在椭圆上.故-2≤y0≤2,所以变成了y轴上在[-2,2]间的线段 说明:注意变形的等价性
网址:http://m.1010jiajiao.com/timu_id_569384[举报]
. (本小题满分12分)
已知椭圆![]() 上任意一点到两焦点距离之和为4,直线
上任意一点到两焦点距离之和为4,直线![]() 为该椭圆的一条准线.
为该椭圆的一条准线.
1)求椭圆C的方程;
2)设直线![]() 与椭圆C交于不同的两点
与椭圆C交于不同的两点![]() 且
且![]() (其中
(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
已知椭圆 上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
(I)求椭圆C的方程;
(II)设直线l:y=kx+2与椭圆C交于不同的两点A、B,且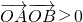 (其中O为坐标原点),求直线l的斜率k的取值范围.
(其中O为坐标原点),求直线l的斜率k的取值范围.
查看习题详情和答案>>
已知椭圆 上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
(I)求椭圆C的方程;
(II)设直线l:y=kx+2与椭圆C交于不同的两点A、B,且 (其中O为坐标原点),求直线l的斜率k的取值范围.
(其中O为坐标原点),求直线l的斜率k的取值范围.
查看习题详情和答案>>
 上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.(I)求椭圆C的方程;
(II)设直线l:y=kx+2与椭圆C交于不同的两点A、B,且
 (其中O为坐标原点),求直线l的斜率k的取值范围.
(其中O为坐标原点),求直线l的斜率k的取值范围.查看习题详情和答案>>