网址:http://m.1010jiajiao.com/timu_id_535708[举报]
一、选择题:(本大题共10个小题;每小题5分,共50分。)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
B
D
C
A
B
C
B
D
B
二、填空题:(本大题共5小题,每小题5分,共25分。)
11.  12.
12.  13.
13. 14.
14.  15. [-1,1]
15. [-1,1] 
三、解答题:(本大题共6小题,共75分。)
16.解:(I)∵u∥v,∴即 ------(2分)
------(2分)
又
 ---------(5分)
---------(5分)
(II)由(I)知 ------------------------(7分)
------------------------(7分)

 ------------------------------------------------(10分)
------------------------------------------------(10分)
又
∴当A- =0,即A=
=0,即A=  时,
时, 的最大值为
的最大值为 --------------(12分)
--------------(12分)
17. 解:(Ⅰ)设A表示甲命中目标,B表示乙命中目标,则A、B相互独立,且P(A)= ,从而甲命中但乙未命中目标的概率为
,从而甲命中但乙未命中目标的概率为
 ------------------------(5分)
------------------------(5分)
(Ⅱ)设A1表示甲在两次射击中恰好命中k次,B1表示乙有两次射击中恰好命中l次。依题意有

由独立性知两人命中次数相等的概率为

18. 解法一:(1)分别延长AC,A1D交于G. 过C作CM⊥A
∵BC⊥平面ACC
∴BM⊥A
平面A
∴CG=2,DC=1 在直角三角形CDG中,

 ,
,
即二面角B―A1D―A的大小为 ------------------------(6分)
------------------------(6分)
(2)在线段AC上存在一点F,使得EF⊥平面A1BD其位置为AC中点,证明如下:
∵A1B
∵由(1)BC⊥平面A
∵EF在平面A
同理可证EF⊥BD, ∴EF⊥平面A1BD------------------------(11分)
∵E为定点,平面A1BD为定平面,点F唯一------------------------(12分)
解法二:(1)∵A1B
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2) ------------------------(2分)
 设平面A1BD的法向量为
设平面A1BD的法向量为


平面ACC =(1,0,0)
------------------------(4分)
=(1,0,0)
------------------------(4分)

即二面角B―A1D―A的大小为 ------------------------(6分)
------------------------(6分)
(2)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD
欲使EF⊥平面A1BD 由(2)知,当且仅当 //
// ---------------(9分)
---------------(9分)


∴存在唯一一点F(0,1,0)满足条件. 即点F为AC中点------------(12分)
19.解:(1) ,
-----------------(2分)
,
-----------------(2分)
因为函数 在
在 处的切线斜率为-3,
处的切线斜率为-3,
所以 ,即
,即 ,------------------------(3分)
,------------------------(3分)
又 得
得 。------------------------(4分)
。------------------------(4分)
函数 在
在 时有极值,所以
时有极值,所以 ,-------(5分)
,-------(5分)
解得 ,------------------------------------------(7分)
,------------------------------------------(7分)
所以 .------------------------------------(8分)
.------------------------------------(8分)
(2)因为函数 在区间
在区间 上单调递增,所以导函数
上单调递增,所以导函数 在区间
在区间 上的值恒大于或等于零,------------------------------------(10分)
上的值恒大于或等于零,------------------------------------(10分)
则 得
得 ,
,
所以实数 的取值范围为
的取值范围为 .----------------------------------(13分)
.----------------------------------(13分)
20.解: (1)由 知,数列{
知,数列{ }为等差数列,设其公差为d,则d=
}为等差数列,设其公差为d,则d= ,
,
故 .------------------------(4分)
.------------------------(4分)
(2)由 ≥0,解得n≤5.故
≥0,解得n≤5.故
当n≤5时, =|
=| |+|
|+| |+…+|
|+…+| |=
|= +
+ +…+
+…+ =
= ;---------------(6分)
;---------------(6分)
当n>5时, =|
=| |+|
|+| |+…+|
|+…+| |=
|= +
+ +…+
+…+ -…-
-…- =
= .--(8分)
.--(8分)
(3)由于 =
= ,
,
所以 ,------(10分)
,------(10分)
从而 >0. ----------------------(11分)
>0. ----------------------(11分)
故数列 是单调递增的数列,又因
是单调递增的数列,又因 是数列中的最小项,要使
是数列中的最小项,要使 恒成立,则只需
恒成立,则只需 成立即可,由此解得m<8,由于m∈Z,
成立即可,由此解得m<8,由于m∈Z,
故适合条件的m的最大值为7. ------------------------(13分)
21. 解:(Ⅰ)设双曲线方程为 (
( ,
, ),
),
则 ,
,
 ,∴
,∴ .------------------------(2分)
.------------------------(2分)
又 在双曲线上,∴
在双曲线上,∴ .
.
联立①②③,解得 ,
, .∴双曲线方程为
.∴双曲线方程为 .--------(5分)
.--------(5分)
注:对点M用第二定义,得 ,可简化计算.
,可简化计算.
(Ⅱ) ,设
,设 ,
, ,m:
,m: ,则
,则
由 ,得
,得 ,
, .--------------------(7分)
.--------------------(7分)
由 ,得
,得 .
.
∴ ,
, .
. .
.
由 ,
, ,
, ,---------------------(9分)
,---------------------(9分)
消去 ,
, ,
,
得 .------------------------(10分)
.------------------------(10分)
∵ ,函数
,函数 在
在 上单调递增,
上单调递增,
∴ ,∴
,∴ .------------------------(11分)
.------------------------(11分)

 ,其
,其 中为常数,
中为常数, .
. 时,求曲线
时,求曲线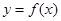 在点
在点 处的切线方程;
处的切线方程; 的极大值为
的极大值为 ?若存在,求出
?若存在,求出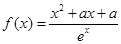 ,其
,其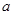 中为常数,
中为常数,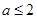 .
.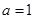 时,求曲线
时,求曲线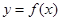 在点
在点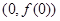 处的切线方程;
处的切线方程;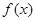 的极大值为
的极大值为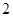 ?若存在,求出
?若存在,求出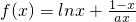 ,其中a为大于零的常数.
,其中a为大于零的常数.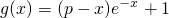 ,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求实数p的取值范围.(e为自然对数的底)
,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求实数p的取值范围.(e为自然对数的底) ,其中a为大于零的常数.
,其中a为大于零的常数. ,若存在x∈[1,e],使不等式g(x)≥lnx成立,求实数p的取值范围.(e为自然对数的底)
,若存在x∈[1,e],使不等式g(x)≥lnx成立,求实数p的取值范围.(e为自然对数的底)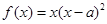 ,
,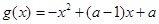 (其中
(其中 为常数).
为常数).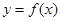 和
和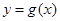 有相同的极值点,求
有相同的极值点,求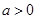 ,问是否存在
,问是否存在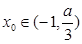 ,使得
,使得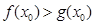 ,若存在,请求出实数
,若存在,请求出实数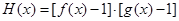 ,若函数
,若函数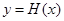 有5个不同的零点,求实数
有5个不同的零点,求实数