摘要:6.a.b为异面直线.且分别在平面α.β内.若α∩β=I.则直线lA.至少与a.b之一平行 B.至多与a.b之一相交C.与a.b都不平行 D.至少与a.b之一相交
网址:http://m.1010jiajiao.com/timu_id_510268[举报]
 在平面直角坐标系xOy中,已知椭圆E:
在平面直角坐标系xOy中,已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆E的标准方程;
(2)若点A,B分别是椭圆E的左、右顶点,直线l经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,直线AP交l于点M,设直线OM的斜率为k1,直线BP的斜率为k2,求证:k1k2为定值.
在平面直角坐标系xOy中,设椭圆
+
=1(a>b>0)的上、下顶点为S,T点E在椭圆上且异于S,T两点,直线SE与TE的斜率之积为-4O为坐标原点
(1)求椭圆的离心率;
(2)若椭圆以F1(0,-
)和F2(0,
)为焦点,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x轴,y轴的交点分别为A,B,且向量
=
+
求:点M的轨迹方程及|OM|的最小值.
查看习题详情和答案>>
| y2 |
| a2 |
| x2 |
| b2 |
(1)求椭圆的离心率;
(2)若椭圆以F1(0,-
| 3 |
| 3 |
| OM |
| OA |
| OB |
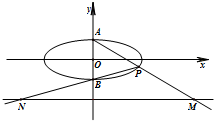 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.