摘要:则V=. ------ 7分(Ⅱ)∵PA=CA.F为PC的中点.∴AF⊥PC. ------8分∵PA⊥平面ABCD.∴PA⊥CD.∵AC⊥CD.PA∩AC=A.∴CD⊥平面PAC.∴CD⊥PC. ∵E为PD中点.F为PC中点.∴EF∥CD.则EF⊥PC. --- 12分∵AF∩EF=F.∴PC⊥平面AEF.-- 14分
网址:http://m.1010jiajiao.com/timu_id_497708[举报]
在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,
求⑴ ∠ADB的大小;⑵ BD的长.

【解析】本试题主要考查了三角形的余弦定理和正弦定理的运用
第一问中,∵cos∠ADC=
= =-
=- ∴ cos∠ADB=cos(180°-∠ADC)=-cos∠ADC=
∴ cos∠ADB=cos(180°-∠ADC)=-cos∠ADC= ∴ cos∠ADB=60°
∴ cos∠ADB=60°
第二问中,结合正弦定理∵∠DAB=180°-∠ADB-∠B=75°
由 =
=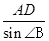 得BD=
得BD= =5(
=5( +1)
+1)
解:⑴ ∵cos∠ADC=
= =-
=- ,……………………………3分
,……………………………3分
∴ cos∠ADB=cos(180°-∠ADC)=-cos∠ADC= ,
……………5分
,
……………5分
∴ cos∠ADB=60° ……………………………6分
⑵ ∵∠DAB=180°-∠ADB-∠B=75° ……………………………7分
由 =
=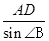 ……………………………9分
……………………………9分
得BD= =5(
=5( +1)
+1)
查看习题详情和答案>>
今有一组实验数据如下:
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| v | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
现准备用下列函数其中的一个近似地表示这些数据满足的规律:①v=log2t;②v=log![]() t;③v=
t;③v=![]() ;④v=2t-2.则其中最接近一个是________.(填上代表函数的序号)
;④v=2t-2.则其中最接近一个是________.(填上代表函数的序号)